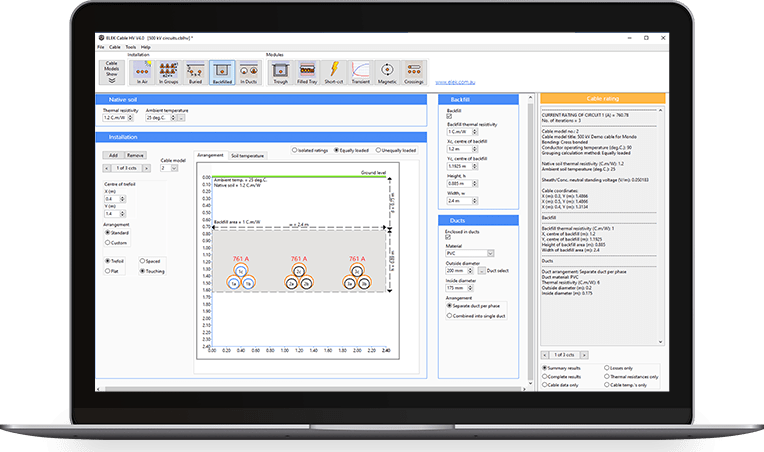
Overview
This paper describes the method and has examples for calculating the steady-state current rating of cables installed in ventilated tunnels. In the examples, multiple cable circuits installed in a ventilated tunnel are simulated and the effects of varying parameters such as depth of tunnel axis, length of tunnel and air velocity inside the tunnel on the cable current ratings are shown.
The calculations were performed using ELEK Cable High Voltage™ Software
IEC calculation method for ventilated tunnels
The Standard IEC 60287-2-3 [1] details a methodology to calculate the steady-state current rating for cables of all voltages installed in tunnels with natural or forced ventilation. The method is based on the calculation of the temperature of the cable surface, the air in the tunnel and the tunnel wall as a function of the heat generated by the cables. Consideration of longitudinal temperature gradients is involved as the moving air inside the tunnel (assumed to be either laminar or turbulent depending on the air velocity) removes heat from the cables. Longitudinal heat transfer within the cables and the surroundings of the tunnel on the other hand is assumed to be negligible and heat generated by a cable is assumed to be constant along its length.
The method is applicable to any type of cable and for multiple circuits. Where multiple circuits are involved, their characteristics are assumed to be identical. Only steady state conditions are considered, where the inlet air temperature and the cable loading are constant for a sufficient time for steady temperatures to be achieved.
The current rating of cables inside a tunnel depends on the air temperature. The longitudinal air movement in the tunnel dissipates heat from the cable surface along the tunnel axis. This creates an increase in air temperature along the tunnel axis as we move away from the inlet. The following heat transfer mechanisms are considered:
- Radial conduction within the cable.
- Radiation from the cable surface to the tunnel wall.
- Convection from the cable surface to the air inside the tunnel.
- Convection from the air inside the tunnel to the tunnel wall.
- Longitudinal heat transfer by convection resulting from air flow (laminar or turbulent depending on velocity).
A thermal network representing slices of the tunnel cross section, is considered and the slices are linked by the longitudinal heat transfer of the air flow along the tunnel. A delta-star transformation is applied on ever slice to derive a thermal network with one thermal resistance each between the star point and the cable surface, the tunnel wall, and the ventilating air respectively. This results in a fictitious increase of the ambient temperature to account for the ventilation. The equivalent thermal resistance of the cable surrounding is calculated (iteratively) and used in the steady state calculations to obtain the current rating.
Example calculations
Cable model
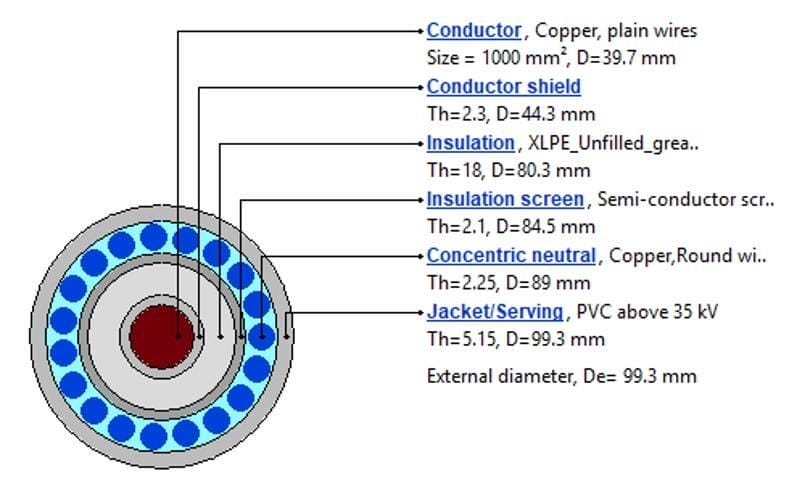
The cable model considered in this study is a 132 kV 1000 mm2single core cable as shown in Figure 1. The cable has an outer diameter of 99.3 mm.
Tunnel parameters
The tunnel considered in this study has the following parameters.
| Parameter | Value | Unit |
|---|---|---|
| Native soil thermal resistivity | 1.852 | K.m/W |
| Tunnel shape | Circular | - |
| Tunnel outer diameter | 3.2 | m |
| Tunnel inner diameter | 3 | m |
| Tunnel wall thermal resistivity | 1 | K.m/W |
| Temperature at the ground level | 25 | oC |
| Temperature at tunnel inlet | 40 | oC |
Arrangement of the circuits
The cables circuits are arranged in trefoil and spaced vertically along the inner edges of the tunnel wall as shown in Figure 2. This image was taken from ELEK Cable HV™ Software.

Variation of current rating with tunnel length
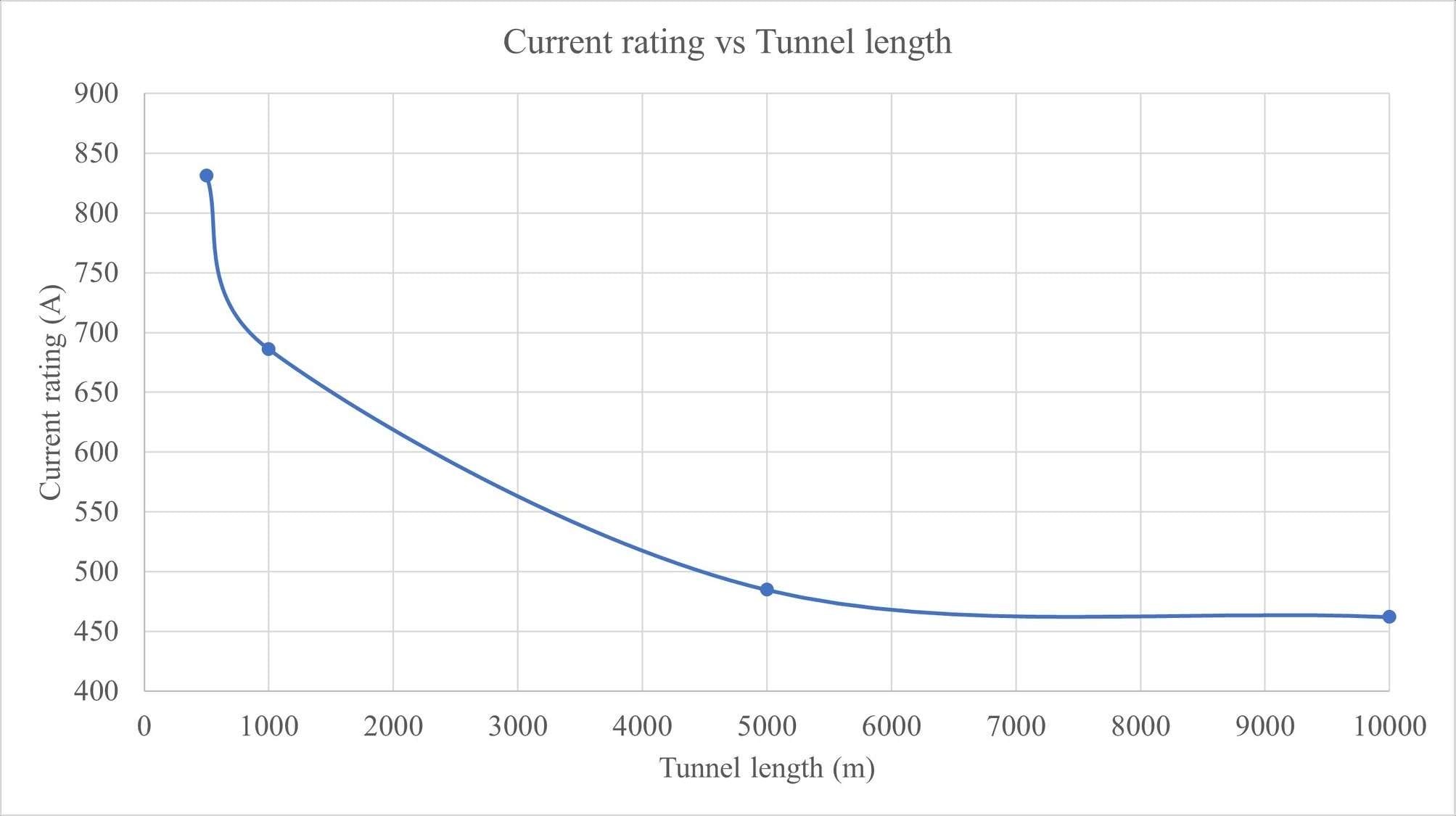
The length of tunnel is varied and its impact on the current rating was examined. The different tunnel lengths considered were 500 m, 1 km, 5km and 10 km. The tunnel axis is at 2m below the ground surface and the air velocity inside the tunnel is 2 m/s.
The results shown in Figure 3 indicates with increasing tunnel length there is a non-linear reduction in cable current rating. The total variation in cable current rating between the 500 m tunnel and the 10 km tunnel is 44%.
Variation of current rating with air velocity
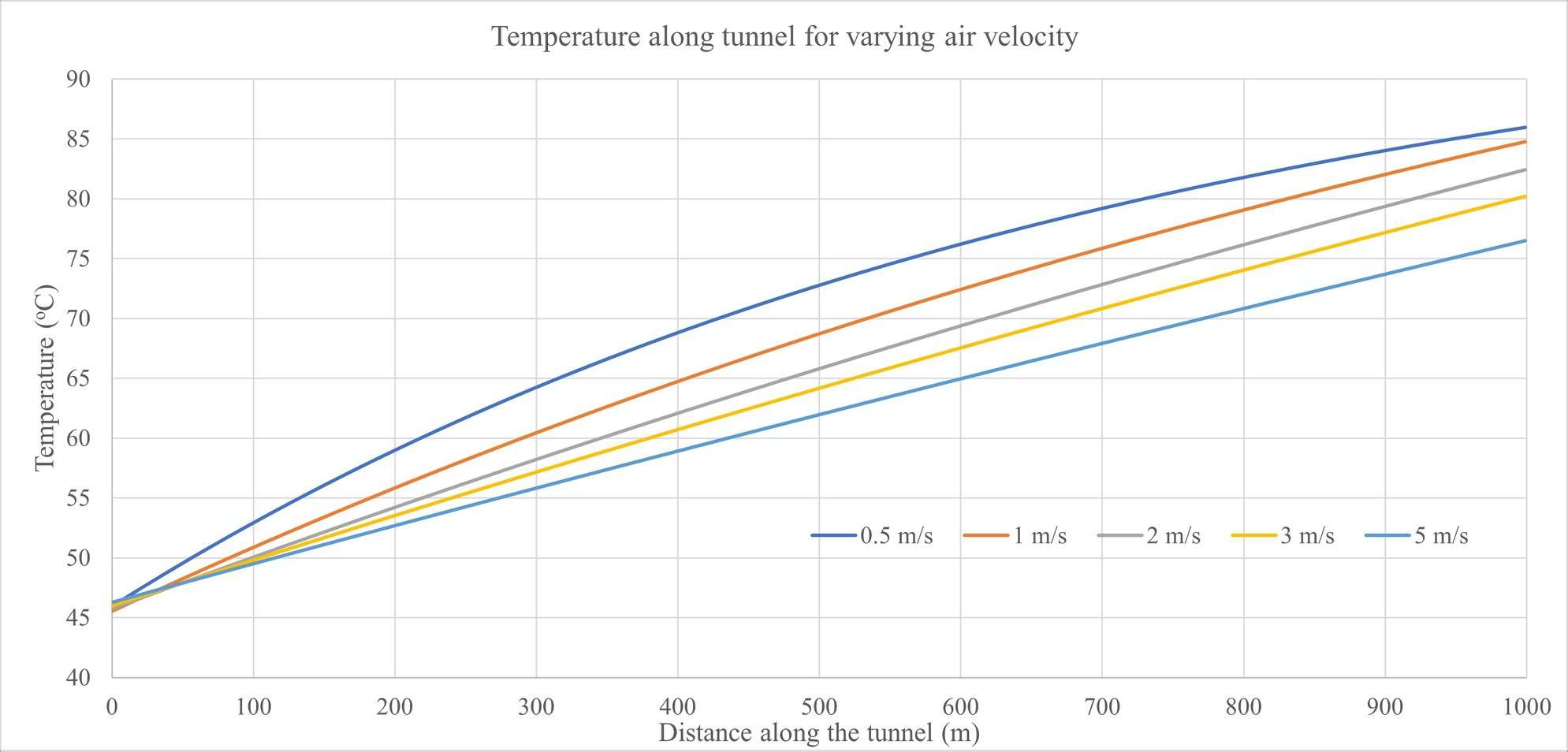
The air velocity inside the tunnel which is assumed to be constant along the length of the tunnel was varied between 0.5 m/s and 5 m/s. As air velocity increases the longitudinal heat transfer along the tunnel length increases. This tends to cool the cables down which in-turn increases their current carrying capacity. The fixed tunnel parameters were length 1000 m and tunnel axis 2 m below the ground surface.
Table 2 shows that as air velocity increases the temperatures inside the tunnel decrease which increases cable current rating. Figure 4 shows how cable surface temperature (correlated with cable current rating) varies with change in air velocity inside a tunnel. The percentage increase of the current rating between a tunnel air velocity of 0.5 m/s and 5 m/s was 45%.
| Air velocity inside the tunnel (m/s) |
Tunnel air temperature, θat (oc) |
Tunnel wall temperature, θt (oc) |
Cable surface temperature, θs (oc) |
Current rating of cables (A) |
|---|---|---|---|---|
| 0.5 | 83.069 | 81.679 | 85.972 | 497.8 |
| 1 | 80.841 | 80.360 | 84.777 | 569.47 |
| 2 | 77.436 | 77.618 | 82.406 | 686.23 |
| 3 | 74.658 | 75.056 | 80.179 | 776.08 |
| 5 | 70.430 | 70.941 | 76.492 | 907.74 |
Variation of current rating with depth of tunnel axis
The depth of the tunnel axis was changed and its impact on the current rating investigated. The tunnel axis depth was varied to 2 m, 4 m and 5 m. The length of the tunnel was fixed at 1000m with constant air velocity of 2 m/s. Table 3 shows for deeper tunnel depth the cable current rating was reduced but not by too much. The percentage reduction of the current rating between a tunnel with only 2 m depth compared with 5 m depth was under 5 %.
| Depth of tunnel axis (m) |
Tunnel air temperature, θat (oc) |
Tunnel wall temperature, θt (oc) |
Cable surface temperature, θs (oc) |
Current rating of cables (A) |
|---|---|---|---|---|
| 2 | 77.436 | 77.618 | 82.406 | 686.23 |
| 4 | 78.217 | 79.09 | 83.073 | 657.77 |
| 5 | 78.360 | 79.360 | 83.196 | 657.77 |
Conclusion
A computer software implementation of the IEC standards for calculating cable current ratings in ventilated tunnels has allowed this common installation method to be modelled. Multiple cable circuits installed inside the same tunnel can be modelled simultaneously.
A parametric study involving varying certain tunnel model parameters has revealed whether their effects on the cable current rating results are significant or not so. For example, the overall length of the tunnel and the air velocity inside of the tunnel both have significant impact on cable current ratings whilst tunnel depth does not.
References
IEC 60287-2-3 Edition 1.0 2017-04 Electric cables – Calculation of the current rating – Part 2-3: Thermal resistance – Cables installed in ventilated tunnels