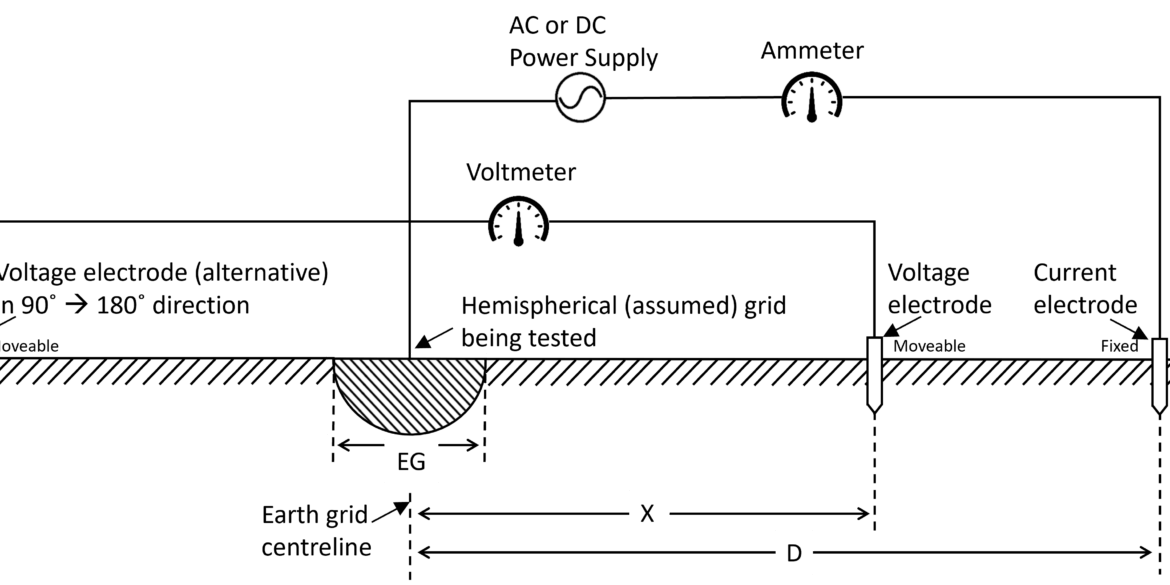
Vue d'ensemble
Une étude approfondie des grilles de mise à la terre a été entreprise à l'aide du logicielSafeGrid Earthing Software conçu pour déterminer la performance des grilles de configuration géométrique arbitraire dans les sols à deux couches. L'étude confirme les travaux de Dawalibi et Mukhedkar réalisés à l'aide du logiciel appelé CDEGS.
Une variété de configurations de grilles de terre et de modèles de sol ont été analysés. Des paramètres physiques importants ont été modifiés et les résultats relatifs à la sécurité ont été calculés, notamment les résistances de terre, l'élévation du potentiel de terre, le toucher et les potentiels d'échelon.
Les résultats de cette étude visent à prouver ce qui suit :
- Les méthodes d'analyse simplifiées telles que les équations présentées dans la norme IEEE 80 font trop d'hypothèses et ne permettent pas de prédire avec précision les performances des systèmes de mise à la terre.
- Les résultats obtenus sont en accord avec la théorie physique et correspondent étroitement aux résultats d'autres recherches et études similaires.
Logiciel
L'algorithme principal de SafeGrid est basé sur des équations électromagnétiques éprouvées et sur la technique des éléments finis, et confirmé par des essais sur le terrain sur plusieurs décennies.
Capacités de modélisation :
- Systèmes de mise à la terre de configurations géométriques arbitraires.
- Modélisation multicouche des sols.
- Analyse tridimensionnelle (3D) des potentiels de surface, de toucher et de pas.
Modèle de sol
Dans ce rapport, deux types de modèles de sol sont utilisés : le sol uniforme et le sol bicouche. Cependant, SafeGrid peut également modéliser des sols multicouches. Se référer à l'article sur la performance des systèmes de mise à la terre dans un sol multicouche.
La modélisation précise d'un système de mise à la terre nécessite l'utilisation d'un modèle de sol à deux couches. En effet, la résistance du sol, les potentiels de pas et de contact sont fonction des couches supérieure et inférieure du sol.
Le modèle bicouche consiste en une couche supérieure de résistivité ρ1 d'épaisseur finie ainsi qu'une couche inférieure de résistivité ρ2 à une profondeur infinie.
La norme IEEE 80 stipule que la représentation d'une électrode de mise à la terre basée sur un modèle de terre équivalente à deux couches est suffisante pour concevoir un système de mise à la terre sûr.
| Description | Facteur de réflexion,K1 | Résistivité de la couche supérieure, ρ1 (Ω.m) | Résistivité de la couche inférieure, ρ2 (Ω.m) |
|---|---|---|---|
| Uniforme | 0 | 100 | 100 |
| Bas sur haut | 0.9 | 100 | 1900 |
| 0.5 | 100 | 300 | |
| Haut sur bas | -0.9 | 100 | 5.26 |
| -0.5 | 100 | 33.33 |
1 Facteur de réflexion, K = (ρ2 - ρ1)/ (ρ2 + ρ1)
Cas de grille analysés
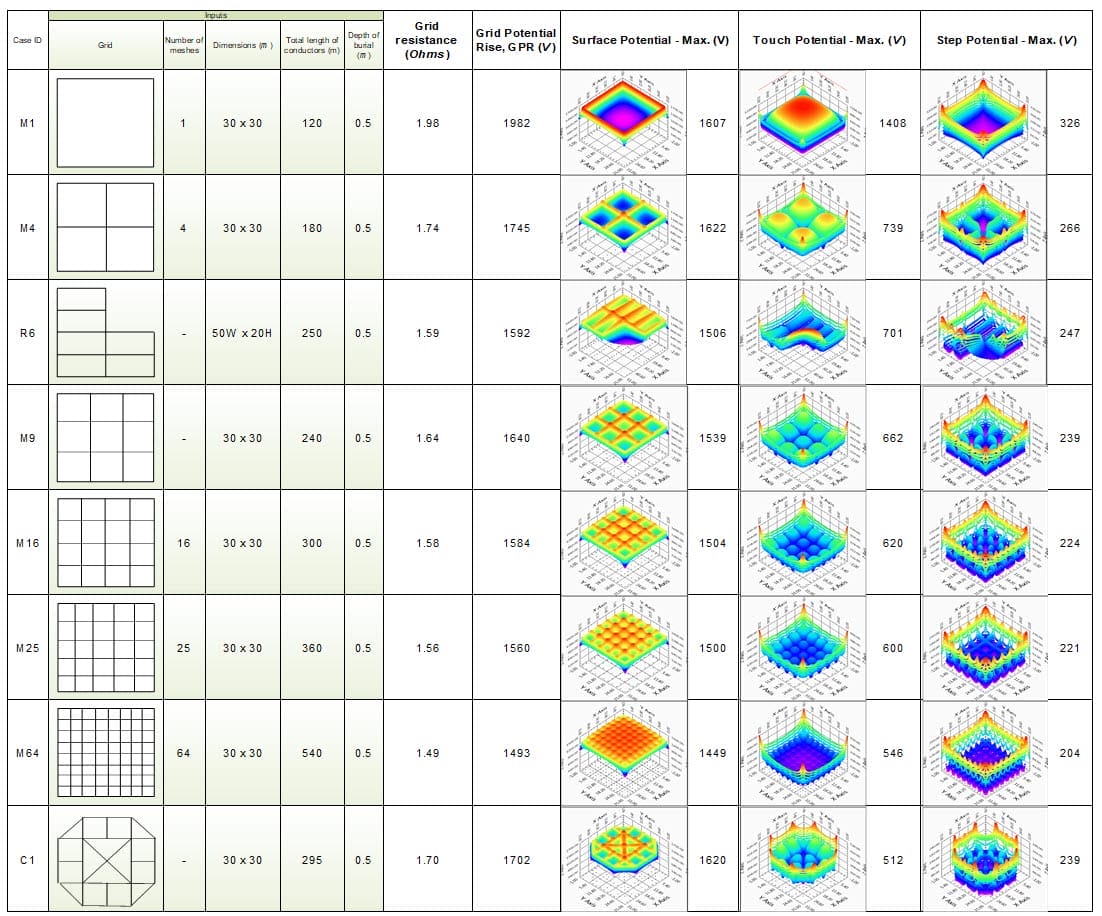
Les grilles de mise à la terre simples présentées dans le tableau 2 ont été analysées en détail.
SafeGrid peut modéliser n'importe quelle configuration arbitraire de conducteur de terre.
Ces grilles de mise à la terre sont généralement constituées de grilles carrées ou rectangulaires dont les mailles contiennent des conducteurs de longueur identique et également espacés.
La profondeur d'enfouissement des grilles de terre a varié de 0,01 m à 100 m. Pour les modèles de sol à deux couches, la profondeur de la couche supérieure a varié de 0,1 m à 100 m.
Les valeurs des résultats de calcul figurant dans le tableau 2 correspondent à des valeurs de paramètres fixes, comme indiqué. Ces paramètres correspondent aux mêmes grilles simples qui ont été modifiées au cours de l'analyse paramétrique.
Résultats
Potentiels de surface, de contact et de pas
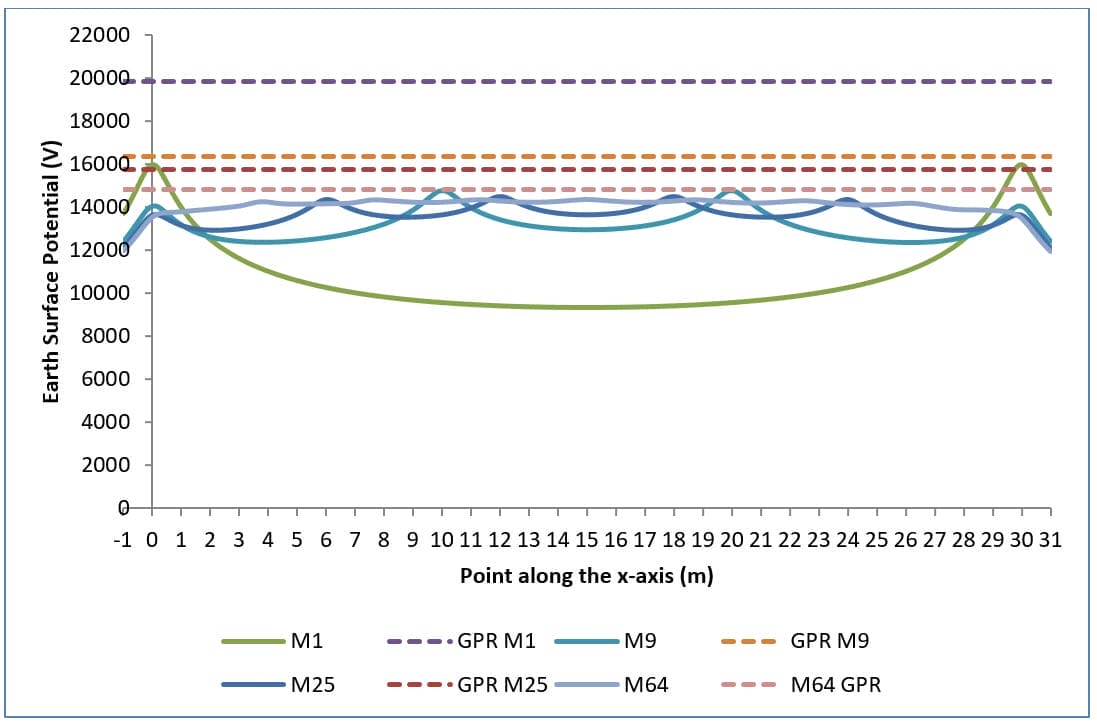
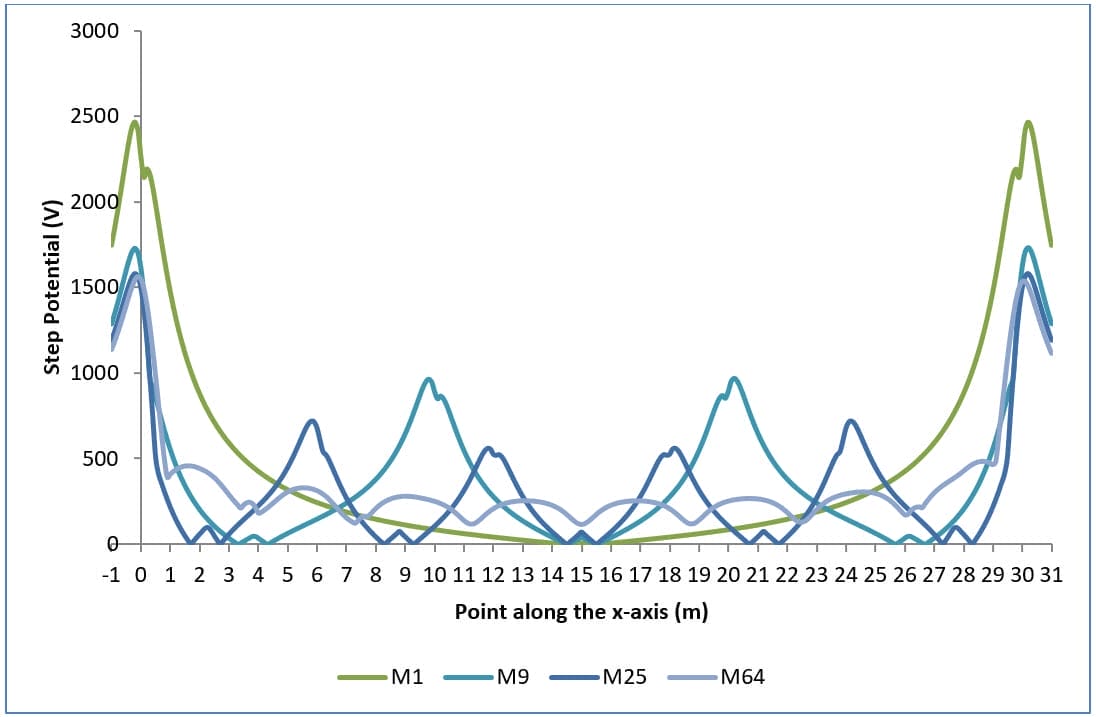
Les graphiques des potentiels de surface, des potentiels de contact et des potentiels d'échelon pour différentes configurations de grille sont présentés dans les figures 1, 2 et 3 respectivement.
L'augmentation du nombre de conducteurs (ou de mailles) a les effets suivants :
- Diminue la résistance du réseau (R).
- Diminue l'augmentation du potentiel du réseau (GPR) puisque GPR = R * courant de défaut.
- Le potentiel maximal de la surface terrestre diminue.
- Les potentiels tactiles sont réduits (figure 2).
- Les pires potentiels de contact se déplacent vers le bord de la grille. L'augmentation de la concavité des courbes de la figure 2 pour l'augmentation du nombre de mailles en est la preuve.
Notez que cette dernière observation s'applique à un sol uniforme, à un facteur de réflexion positif K et à des conducteurs de grille uniformément espacés. Dans le cas contraire, il est difficile de prévoir l'emplacement des pires potentiels de contact.

Densité de courant le long des conducteurs
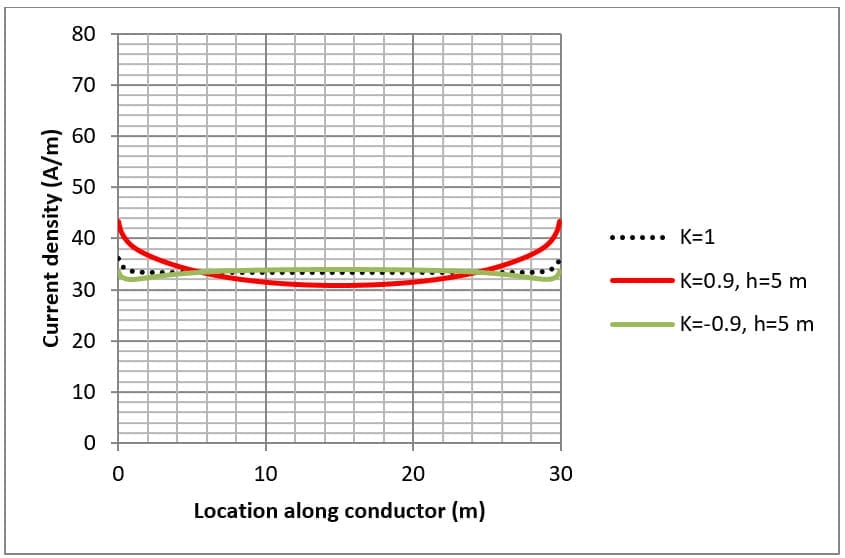
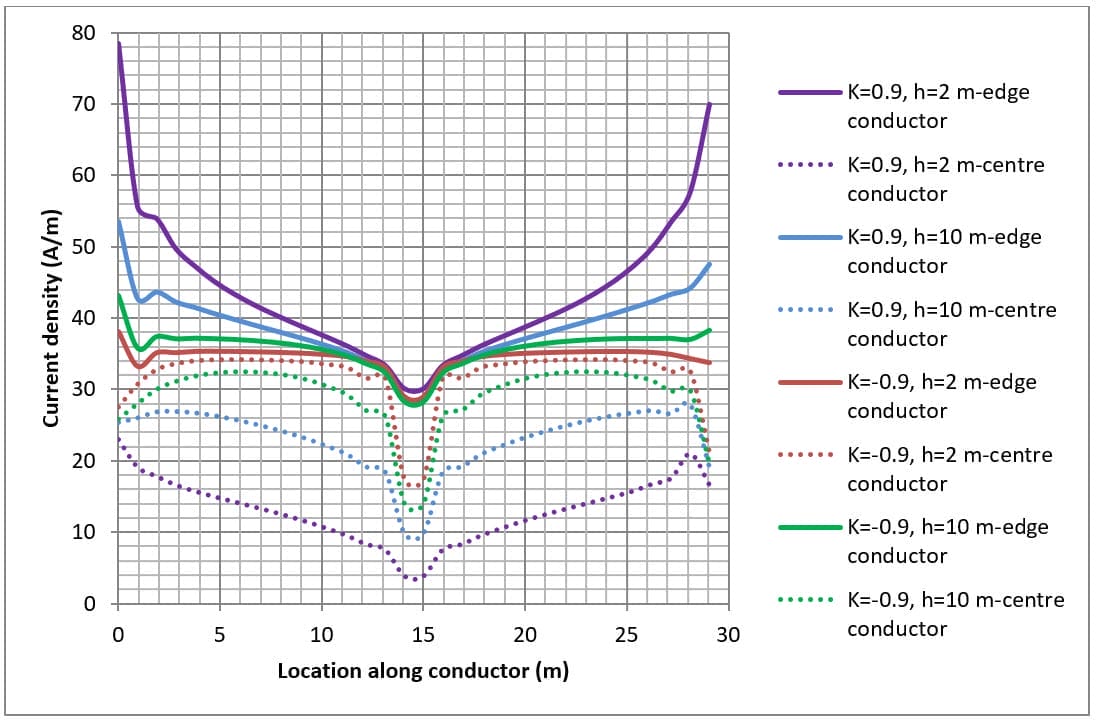
La densité de courant pour les conducteurs est présentée dans les figures 4, 5 et 6 pour différentes dispositions de grille et structures de résistivité du sol.
Le courant de défaut appliqué au réseau dépend de la longueur totale des conducteurs du réseau pour une disposition particulière, 1000 A étant appliqué pour chaque 30 mètres de conducteur. Par exemple, pour une maille unique composée de 4 conducteurs de 30 m, le courant de défaut appliqué est de 4 x 1000 A.
La distribution de la densité de courant le long des conducteurs du réseau n'est pas uniforme mais est une fonction complexe qui varie en fonction :
- Disposition de la grille (c'est-à-dire le nombre de mailles, etc.)
- l'emplacement du conducteur par rapport à d'autres conducteurs ; et
- Structure de résistivité du sol
Lorsque la résistivité de la couche supérieure du sol est inférieure à celle de la couche inférieure (c'est-à-dire K>0), la densité du courant est concentrée vers les extrémités des conducteurs. Cela s'explique par le fait que le courant reste dans la couche supérieure du sol et se propage en se dissipant dans le sol.
When the lower layer soil resistivity is higher than the top layer (i.e. K<0) the current density at the centre of the conductors can be just as high as at the ends. This is because the fault current escapes directly downwards toward the lower resistivity bottom layer.
La dissipation de courant des conducteurs le long du bord est plus élevée (lignes pleines dans la figure 5 et la figure 6) que pour les conducteurs au centre (lignes pointillées dans la figure 5 et la figure 6) de la grille de terre enterrée.

Effet de la couche supérieure du sol sur la résistance de la grille
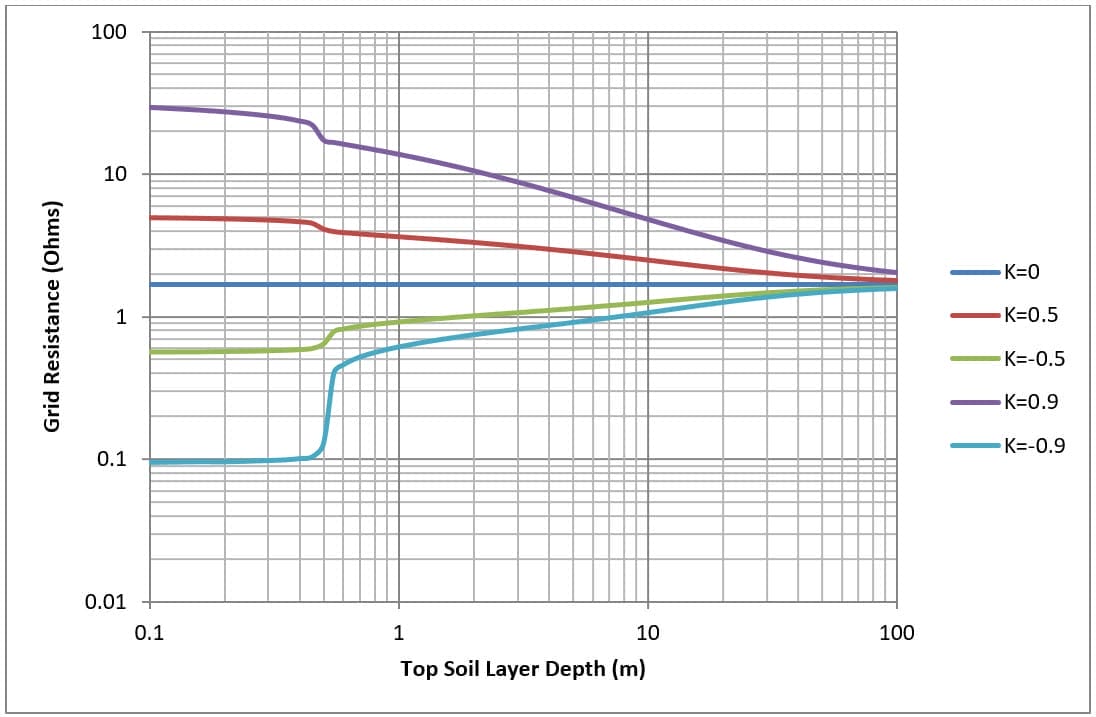
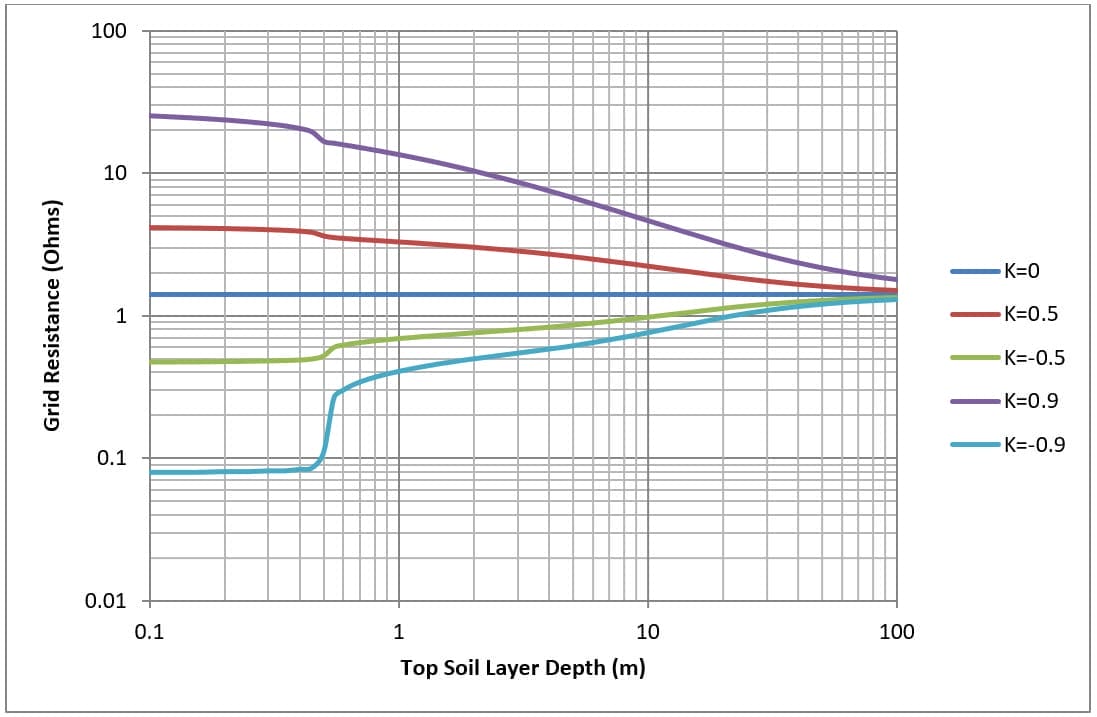
Les figures 7 et 8 montrent, pour une maille simple de 30 x 30 mètres (M4 et M16) enterrée à 0,5 mètre, comment la résistance de la grille varie en fonction de l'épaisseur de la couche supérieure du sol.
La résistivité de la couche supérieure du sol est fixe, tandis que la résistivité de la couche inférieure du sol varie pour obtenir différents facteurs de réflexion (K). La résistance de la grille est calculée pour différentes profondeurs de la couche supérieure du sol.
La modification de la profondeur de la couche supérieure du sol a les effets suivants :
- Pour un modèle de sol uniforme (cas de contrôle), il n'y a pas d'effet sur la résistance de la grille.
- Pour le modèle de sol bas sur haut (K>0), la résistance de la grille diminue au fur et à mesure que la profondeur de la couche supérieure du sol augmente.
- For high on low soil model (K<0) as the depth of the top soil layer is increased grid resistance goes up.
- Lorsque la profondeur de la couche supérieure s'approche de l'infini, la résistance de la grille converge avec le modèle de sol uniforme.
Notez le changement brutal de la résistance de la grille dans tous les cas à une profondeur de 0,5 m de la couche supérieure du sol (qui correspond à la profondeur d'enfouissement de la grille).
Il est démontré que la résistance de la grille est influencée par la couche de sol inférieure, en particulier pour les couches de sol inférieures à forte résistivité (K>0). L'influence de la couche de sol inférieure sur la résistance de la grille peut être négligée à des profondeurs élevées (environ deux fois ou plus le diamètre total de la grille).
Effet de la profondeur d'enfouissement du réseau sur la résistance du réseau
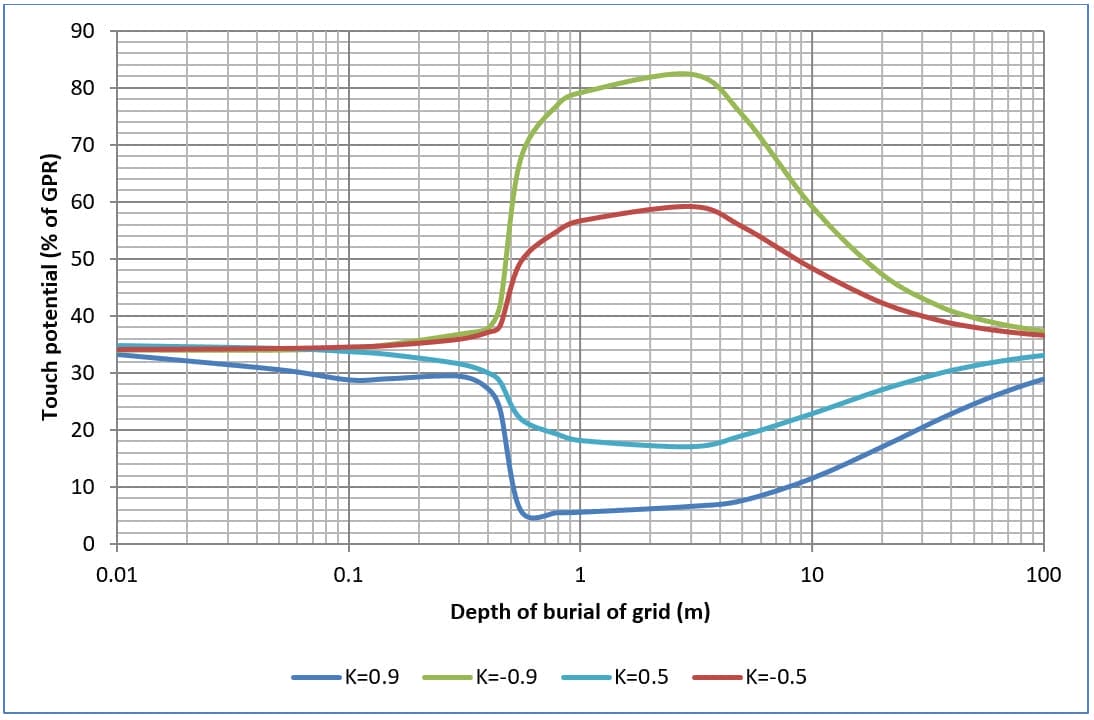
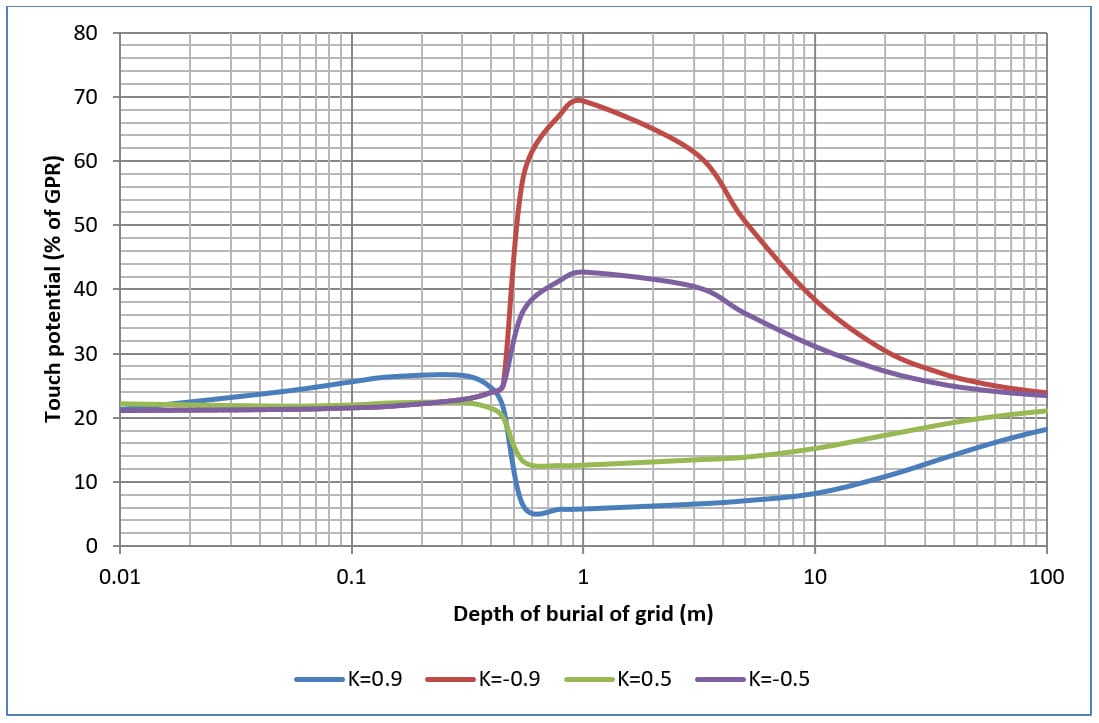
Les figures 9, 10, 11 et 12 montrent les effets sur les potentiels de contact et de pas de la modification de la profondeur d'enfouissement des grilles à quatre et seize mailles dans un sol à deux couches.
En général, avec l'augmentation de la profondeur de l'enfouissement, les potentiels de contact et de pas augmentent jusqu'à une valeur maximale, puis redescendent.
Les potentiels de contact maximaux apparaissent lorsque la résistivité de la couche supérieure du sol est significativement supérieure à la résistivité de la couche inférieure du sol (c'est-à-dire lorsque K=-0,9).
Le potentiel de contact maximal diminue avec l'augmentation du nombre de mailles de la grille.


Conclusions
La détermination précise de la performance du réseau de mise à la terre est impérative pour fournir des conceptions sûres, fonctionnelles et économiques.
Il a été démontré que les paramètres suivants influencent de manière significative le comportement des systèmes de mise à la terre dans des conditions de défaillance :
- Configuration de la grille de mise à la terre.
- Caractéristiques de résistivité du sol.
- Profondeur d'enfouissement de la grille de mise à la terre.
Ces paramètres affectent directement la densité de courant du conducteur (dissipation dans la terre) qui affecte l'élévation du potentiel du réseau (GPR), la résistance du réseau, les potentiels de contact et de pas.
L'accès à des outils logiciels perspicaces permet de concevoir des grilles de mise à la terre optimales et sûres.
Références
IEEE Guide for Safety in AC Substation Grounding, The Institute of Electrical and Electronics Engineers, Inc.
Dawalibi, F., Mise à la terre des lignes de transmission. EL-2699, Projet de recherche 1494-1. Montréal, Québec, Canada, Safe Engineering Services Ltd. 1.
Dawalibi, F. et Mukhedkar, D., "Parametric analysis of grounding grids". IEEE Transactions on Power Apparatus and Systems, Vol.PAS-98, No.5.
Kouteynikoff, P., "Numerical computation of the grounding resistance of substations and towers". IEEE Transactions on Power Apparatus and Systems, Vol.PAS-99, No.3.
Salama, M.M.A. et al, "A formula for resistance of substation grounding grid in two-layer soil". IEEE Transactions on Power Delivery, Vol.10, No.3.