Visión general
Se ha realizado un amplio estudio de las redes de puesta a tierra utilizando el softwareSafeGrid Earthing , diseñado para determinar el rendimiento de redes de configuración geométrica arbitraria en suelos de dos capas. El estudio confirma los trabajos de Dawalibi y Mukhedkar realizados con el software denominado CDEGS.
Se han analizado diversas configuraciones de la red de tierra y modelos de suelo. Se han variado parámetros físicos importantes y se han calculado los resultados relativos a la seguridad, incluidas las resistencias de tierra, el aumento del potencial de tierra y los potenciales de contacto y de paso.
Los resultados de este estudio pretenden demostrar lo siguiente:
- Los métodos simplificados de análisis, como las ecuaciones presentadas en la norma 80 del IEEE, hacen demasiadas suposiciones y no predicen con exactitud el rendimiento de los sistemas de puesta a tierra.
- Los resultados obtenidos concuerdan con la teoría física y concuerdan estrechamente con los resultados de otras investigaciones y estudios similares.
Software
El algoritmo principal de SafeGrid se basa en ecuaciones electromagnéticas probadas y en la técnica de elementos finitos, y se ha confirmado mediante pruebas de campo realizadas a lo largo de varias décadas.
Capacidad de modelización:
- Sistemas de puesta a tierra de configuraciones geométricas arbitrarias.
- Modelización multicapa del suelo.
- Análisis tridimensional (3D) de los potenciales de superficie, tacto y paso.
Modelo de suelo
En este informe se utilizan dos tipos de modelos de suelo: suelo uniforme y suelo de dos capas. Sin embargo, SafeGrid también puede modelar suelos multicapa. Consulte el artículo sobre el rendimiento de los sistemas de puesta a tierra en suelos multicapa.
La modelización precisa de un sistema de puesta a tierra requiere el uso de un modelo de suelo de dos capas. Esto se debe a que la resistencia del suelo y los potenciales de paso y contacto son función de las capas superior e inferior del suelo.
El modelo de dos capas consta de una capa superior de resistividad ρ1 de espesor finito, así como de una capa inferior de resistividad ρ2 a una profundidad infinita.
La norma 80 del IEEE establece que la representación de un electrodo de puesta a tierra basada en un modelo de tierra equivalente de dos capas es suficiente para diseñar un sistema de puesta a tierra seguro.
| Descripción | Factor de reflexión, K1 | Resistividad de la capa superior, ρ1 (Ω.m) | Resistividad de la capa inferior, ρ2 (Ω.m) |
|---|---|---|---|
| Uniforme | 0 | 100 | 100 |
| Bajo en alto | 0.9 | 100 | 1900 |
| 0.5 | 100 | 300 | |
| Alto sobre bajo | -0.9 | 100 | 5.26 |
| -0.5 | 100 | 33.33 |
1 Factor de reflexión, K = (ρ2 - ρ1)/ (ρ2 + ρ1)
Casos analizados
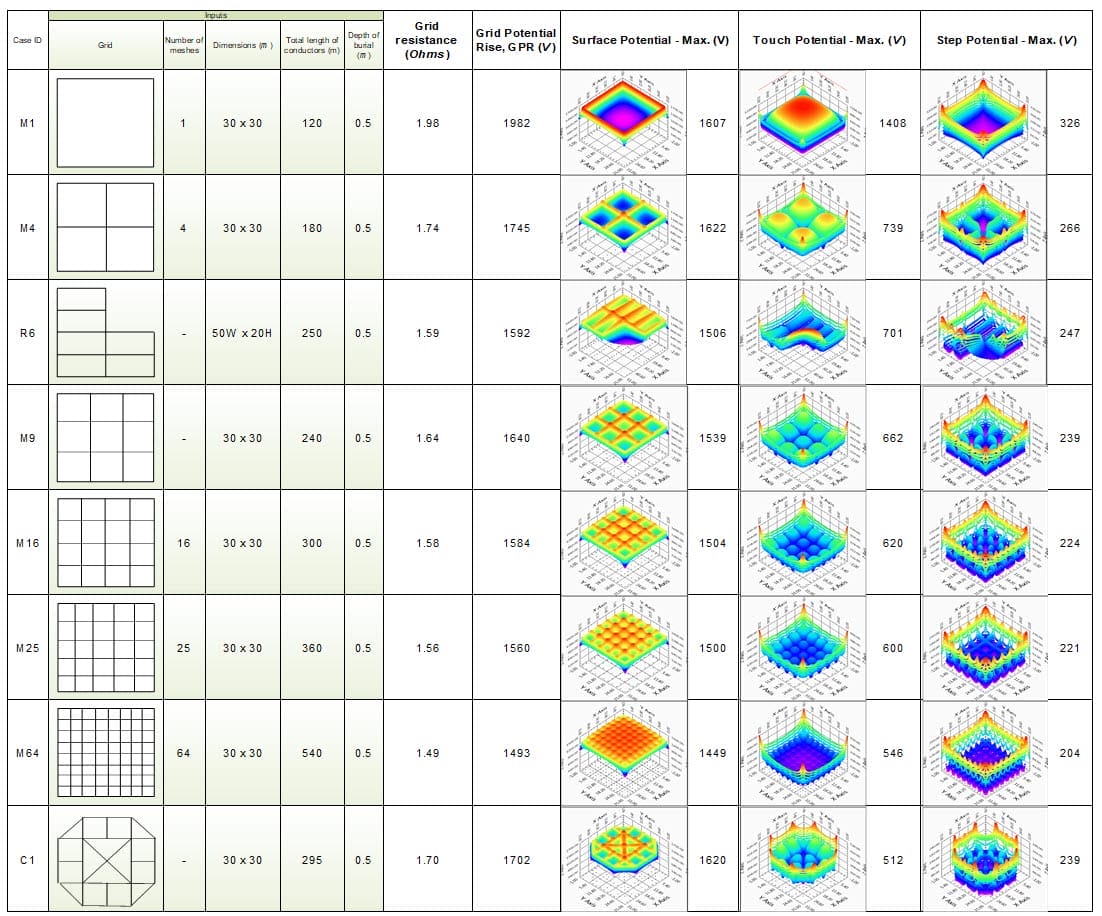
Se analizaron en detalle las redes de puesta a tierra simples que figuran en el cuadro 2.
SafeGrid puede modelar cualquier configuración arbitraria del conductor de puesta a tierra.
Estas rejillas de puesta a tierra consistían generalmente en rejillas cuadradas o rectangulares con mallas que contenían conductores igualmente espaciados y de idéntica longitud.
La profundidad de enterramiento de las rejillas de tierra varió de 0,01 m a 100 m. Para los modelos de suelo de dos capas, la profundidad de la capa superior varió de 0,1 m a 100 m.
Los valores de los resultados de los cálculos que figuran en el cuadro 2 corresponden a valores fijos de los parámetros indicados. Estos parámetros eran para las mismas rejillas simples variadas durante el análisis paramétrico.
Resultados
Potenciales de superficie, tacto y paso
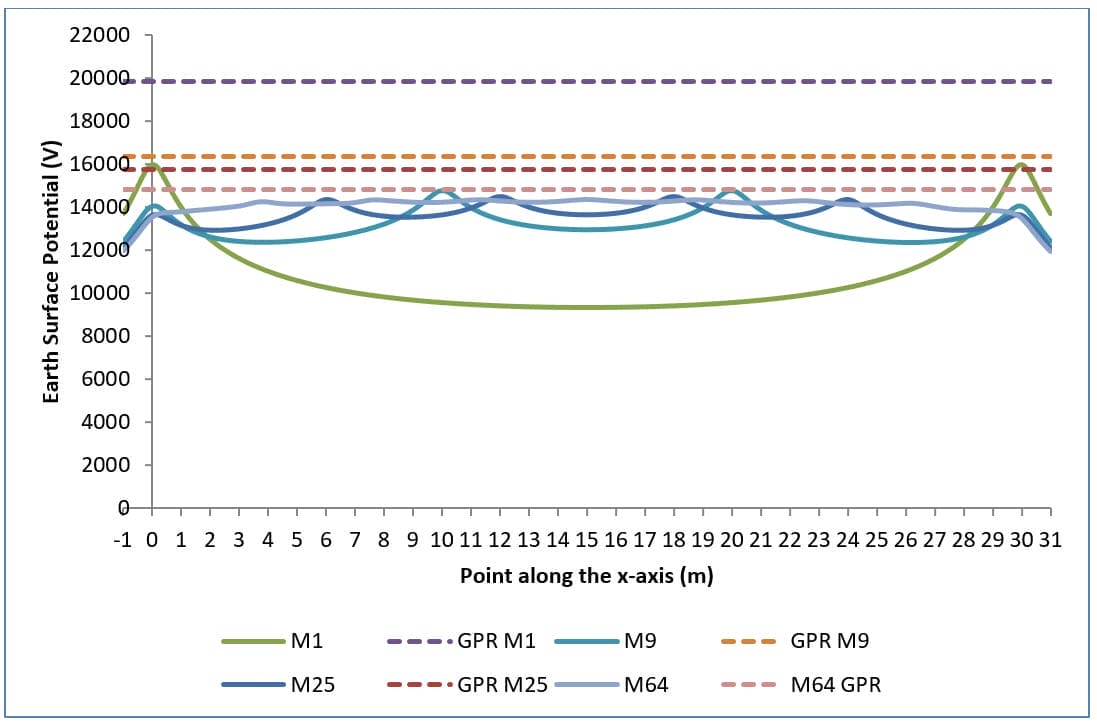
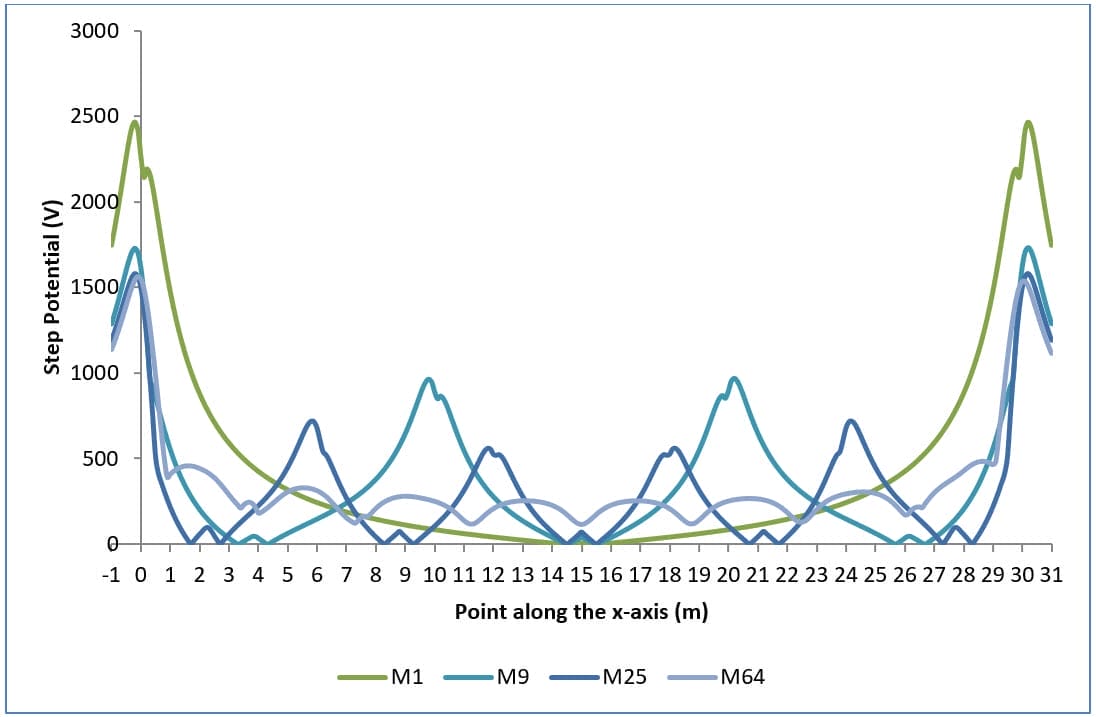
En las figuras 1, 2 y 3 se representan los potenciales de la superficie terrestre, los potenciales de contacto y los potenciales de paso para distintas configuraciones de malla, respectivamente.
Aumentar el número de conductores (o mallas) tiene los siguientes efectos:
- Disminuye la resistencia de red (R).
- Disminuye el aumento del potencial de red (GPR) ya que GPR = R * Corriente de defecto.
- El potencial máximo de la superficie terrestre disminuye.
- Los potenciales táctiles se reducen (Figura 2).
- Los peores potenciales de contacto se desplazan hacia el borde de la malla. Así lo demuestra el aumento de la concavidad de las curvas en la figura 2 al aumentar el número de mallas.
Obsérvese que esta última observación es válida para un suelo uniforme, un factor de reflexión positivo K y conductores de rejilla uniformemente espaciados. De lo contrario, es difícil predecir la ubicación de los peores potenciales de contacto.

Densidad de corriente a lo largo de los conductores
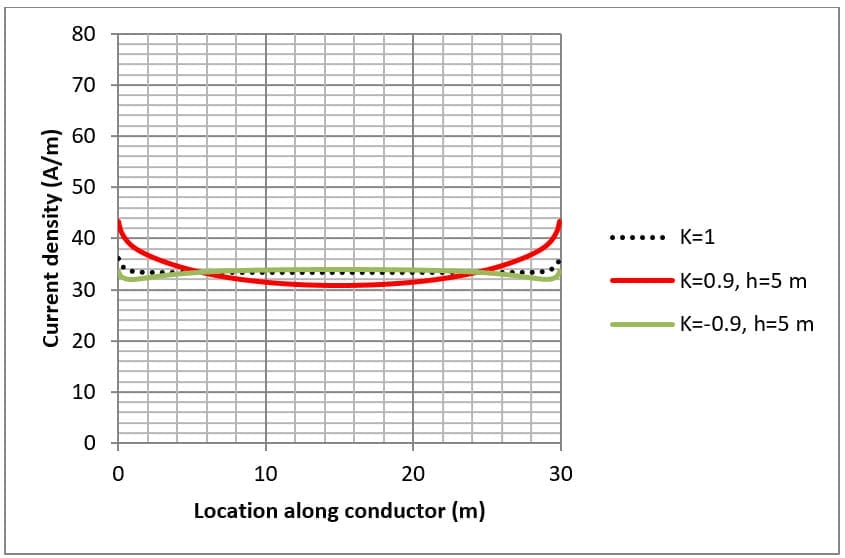
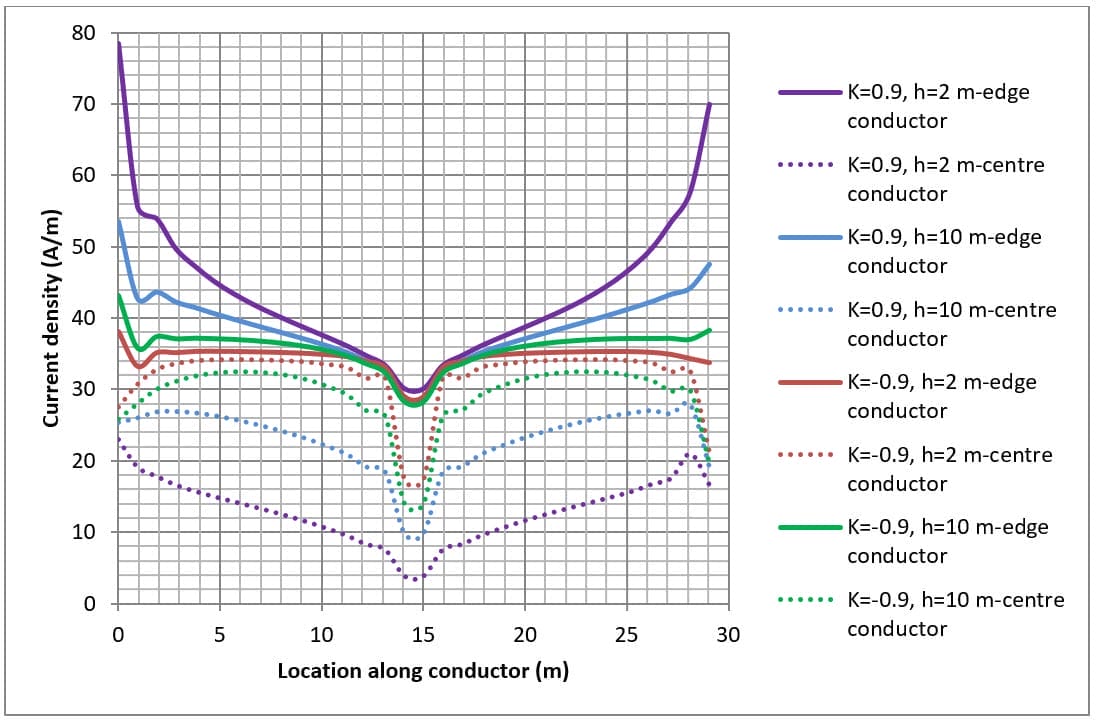
La densidad de corriente de los conductores se muestra en las figuras 4, 5 y 6 para diversas disposiciones de la red y estructuras de resistividad del suelo.
La corriente de defecto en la red aplicada depende de la longitud total de los conductores de la red para una disposición concreta en la que se aplican 1000 A por cada 30 metros de conductor. Por ejemplo, para una malla simple que consta de 4 x 30 m de conductores, la corriente de defecto aplicada es de 4 x 1000 A.
La distribución de la densidad de corriente a lo largo de los conductores de la red no es uniforme, sino que es una función compleja que varía en función de:
- Disposición de la malla (número de mallas, etc.)
- Ubicación del conductor con respecto a otros conductores; y
- Estructura de la resistividad del suelo
Cuando la resistividad del suelo de la capa superior es inferior a la de la capa inferior (es decir, K>0), la densidad de corriente se concentra hacia los extremos de los conductores. Esto se debe a que la corriente permanece dentro de la capa superior del suelo y se dispersa a medida que se disipa en el suelo.
When the lower layer soil resistivity is higher than the top layer (i.e. K<0) the current density at the centre of the conductors can be just as high as at the ends. This is because the fault current escapes directly downwards toward the lower resistivity bottom layer.
La disipación de corriente de los conductores a lo largo del borde es mayor (líneas continuas en la Figura 5 y la Figura 6) que para los conductores en el centro (líneas discontinuas en la Figura 5 y la Figura 6) de la red de tierra enterrada.

Efecto de la capa superior del suelo en la resistencia de la rejilla
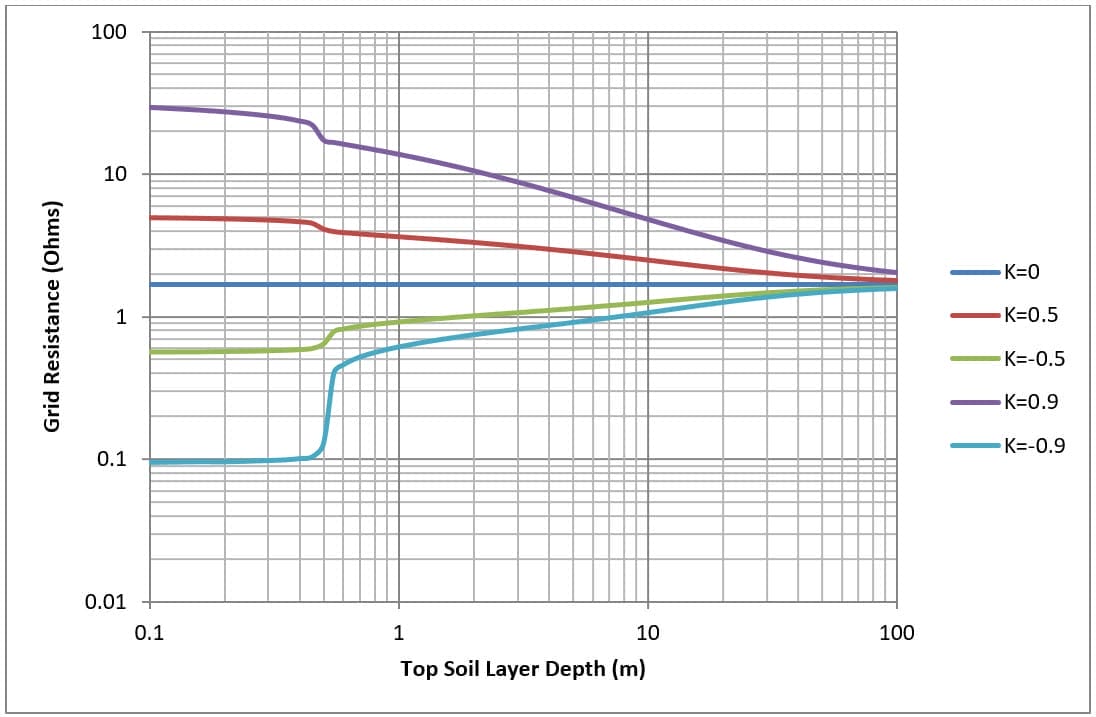
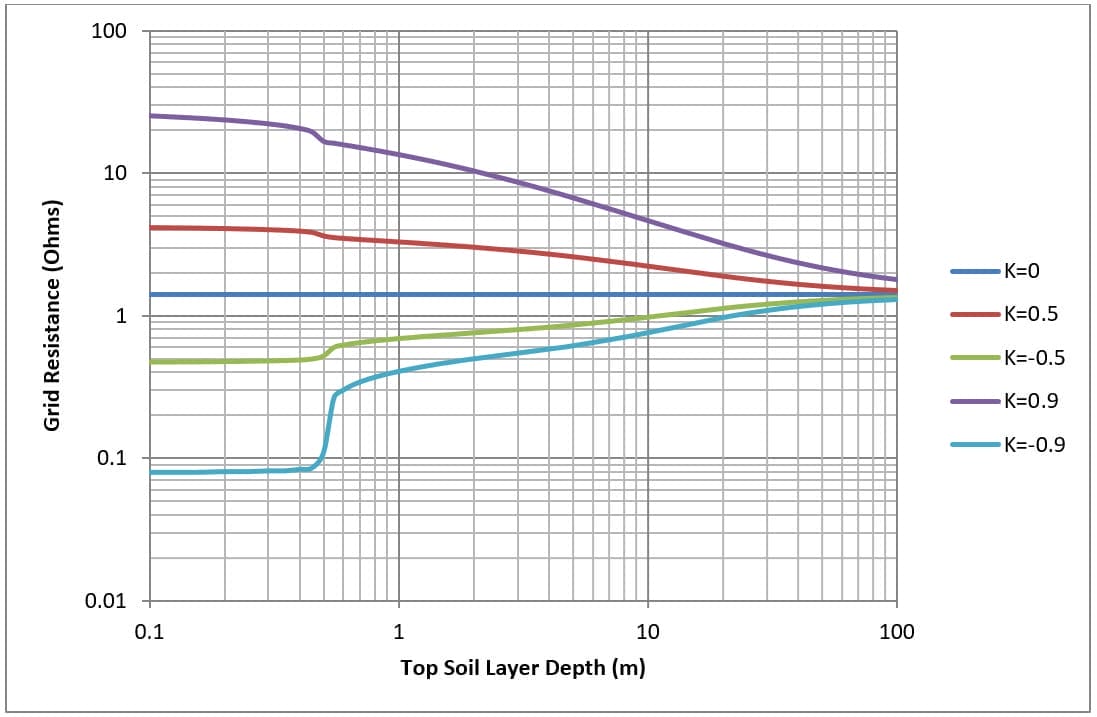
Las figuras 7 y 8 muestran, para una malla simple de 30 x 30 metros (M4 y M16) enterrada a 0,5 metros, cómo varía la resistencia de la rejilla con el espesor de la capa superior del suelo.
La resistividad de la capa superior del suelo es fija, mientras que la de la capa inferior varía para obtener diferentes factores de reflexión (K). La resistencia de la red se calcula para distintas profundidades de la capa superior del suelo.
La modificación de la profundidad de la capa superior del suelo tiene los siguientes efectos:
- Para un modelo de suelo uniforme (caso de control) no hay ningún efecto sobre la resistencia de la red.
- Para el modelo de suelo bajo sobre alto (K>0), a medida que aumenta la profundidad de la capa superior del suelo, disminuye la resistencia de la rejilla.
- For high on low soil model (K<0) as the depth of the top soil layer is increased grid resistance goes up.
- A medida que la profundidad de la capa superior se aproxima al infinito, la resistencia de la malla converge con el modelo de suelo uniforme.
Obsérvese el cambio brusco de la resistencia de la red en todos los casos a una profundidad de la capa superior del suelo de 0,5 m (que corresponde a la profundidad de enterramiento de la red).
Se ha demostrado que la resistencia de la red se ve influida por la capa inferior del suelo, especialmente en el caso de capas inferiores de alta resistividad (K>0). La influencia de la capa inferior del suelo en la resistencia de la rejilla puede despreciarse a grandes profundidades (alrededor de dos o más veces el diámetro total de la rejilla).
Efecto de la profundidad de enterramiento de la red en la resistencia de la red
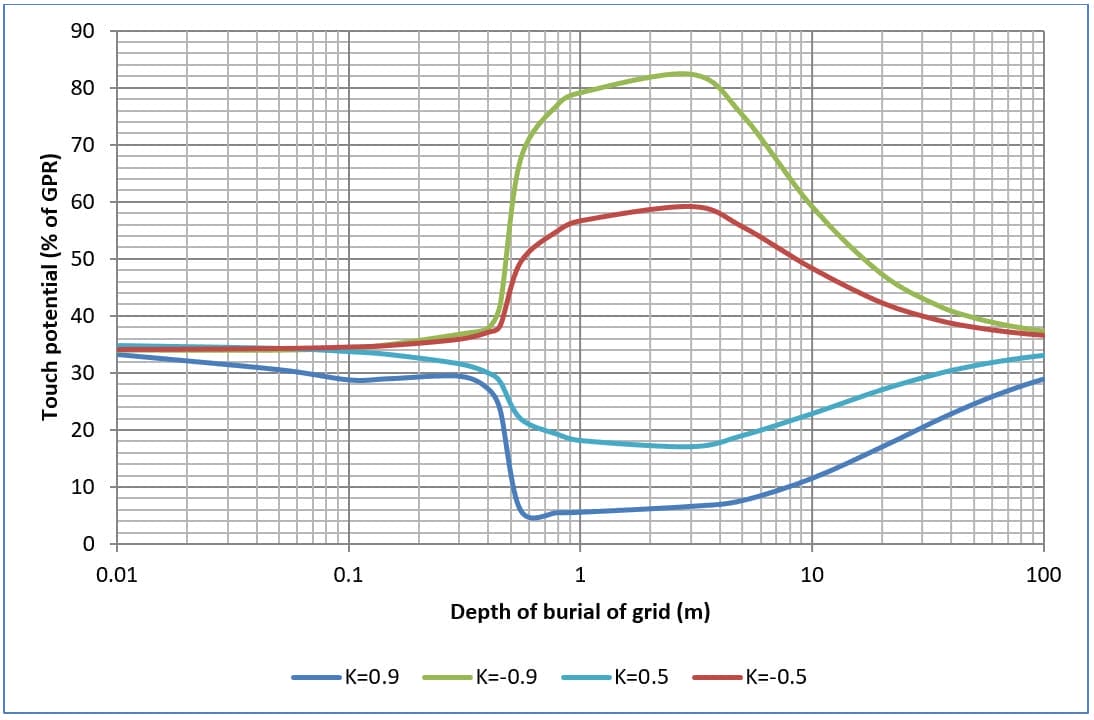
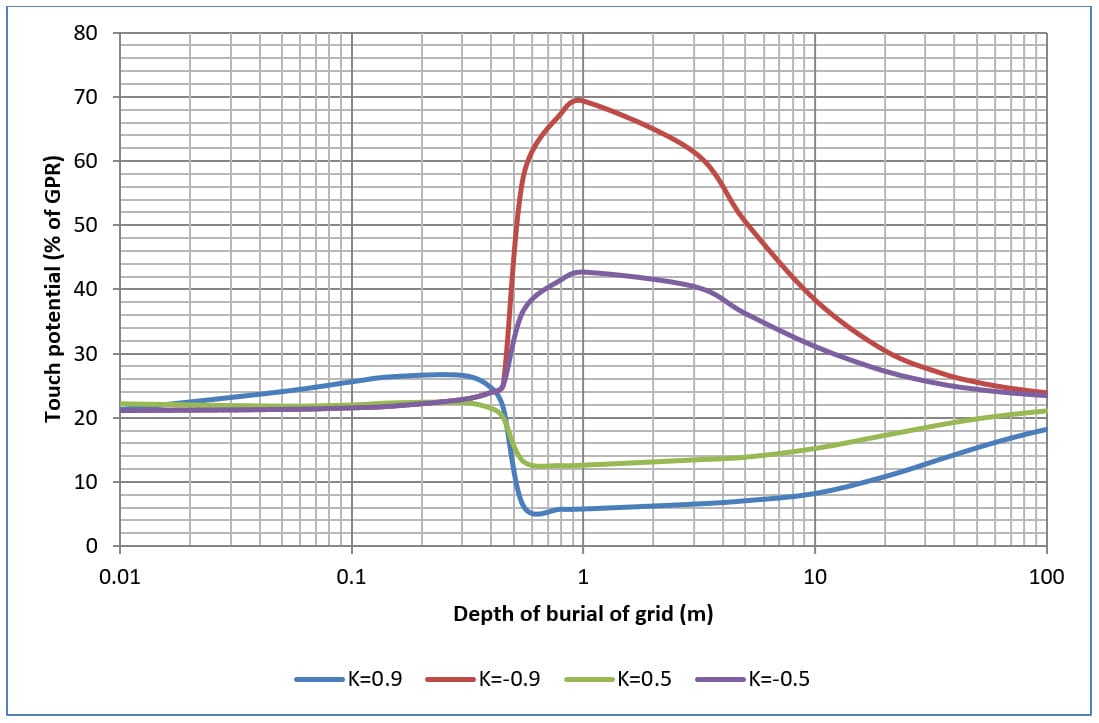
Las figuras 9, 10, 11 y 12 muestran los efectos sobre los potenciales de contacto y de paso al cambiar la profundidad de enterramiento de rejillas de cuatro y dieciséis mallas en un suelo de dos capas.
En general, al aumentar la profundidad del enterramiento, los potenciales de contacto y de paso aumentan hasta un valor máximo y luego vuelven a descender.
Los potenciales de contacto máximos se producen cuando la resistividad del suelo de la capa superior es significativamente mayor que la resistividad del suelo de la capa inferior (es decir, cuando K=-0,9).
El potencial de toque máximo se reduce al aumentar el número de mallas de la cuadrícula.


Conclusiones
La determinación precisa del rendimiento de la red de puesta a tierra es imprescindible para proporcionar diseños seguros, funcionales y económicos.
Se ha demostrado que los siguientes parámetros influyen significativamente en el comportamiento de los sistemas de puesta a tierra en condiciones de fallo:
- Configuración de la red de puesta a tierra.
- Características de resistividad del suelo.
- Profundidad de enterramiento de la red de tierra.
Estos parámetros afectan directamente a la densidad de corriente del conductor (disipación a tierra), que a su vez influye en el aumento del potencial de red (GPR), la resistencia de red y los potenciales de contacto y de paso.
El acceso a herramientas informáticas perspicaces permite diseñar redes de puesta a tierra óptimas y seguras.
Referencias
IEEE Guide for Safety in AC Substation Grounding, The Institute of Electrical and Electronics Engineers, Inc.
Dawalibi, F., Puesta a tierra de líneas de transmisión. EL-2699, Proyecto de investigación 1494-1. Montreal, Quebec, Canadá, Safe Engineering Services Ltd., Canadá. 1.
Dawalibi, F. y Mukhedkar, D., "Parametric analysis of grounding grids". IEEE Transactions on Power Apparatus and Systems, Vol.PAS-98, No.5.
Kouteynikoff, P., "Cálculo numérico de la resistencia de puesta a tierra de subestaciones y torres". IEEE Transactions on Power Apparatus and Systems, Vol.PAS-99, No.3.
Salama, M.M.A. y otros, "A formula for resistance of substation grounding grid in two-layer soil". IEEE Transactions on Power Delivery, Vol.10, No.3.