Übersicht
Es wurde eine umfassende Studie über Erdungsnetze unter Verwendung der SafeGrid Earthing Software durchgeführt, die für die Bestimmung der Leistungsfähigkeit von Netzen mit beliebiger geometrischer Konfiguration in zweischichtigen Böden entwickelt wurde. Die Studie bestätigt die Arbeit von Dawalibi und Mukhedkar, die mit der Software CDEGS durchgeführt wurde.
Es wurde eine Vielzahl von Erdnetzkonfigurationen und Bodenmodellen analysiert. Wichtige physikalische Parameter wurden variiert und sicherheitsrelevante Ergebnisse berechnet, darunter Erdwiderstände, Erdpotentialanstieg, Berührungs- und Stufenpotentiale.
Die Ergebnisse dieser Studie sollen Folgendes belegen:
- Vereinfachte Analysemethoden wie die Gleichungen im IEEE-Standard 80 gehen von zu vielen Annahmen aus und sind nicht in der Lage, die Leistung von Erdungsanlagen genau vorherzusagen.
- Die erzielten Ergebnisse stimmen mit der physikalischen Theorie überein und stimmen eng mit den Ergebnissen anderer ähnlicher Untersuchungen und Studien überein.
Software
Der Hauptalgorithmus von SafeGrid basiert auf bewährten elektromagnetischen Gleichungen und der Finite-Elemente-Methode und wurde in jahrzehntelangen Feldversuchen bestätigt.
Modellierungsfähigkeiten:
- Erdungssysteme mit beliebigen geometrischen Konfigurationen.
- Mehrschichtige Bodenmodellierung.
- Dreidimensionale (3D) Analyse von Oberflächen-, Berührungs- und Stufenpotentialen.
Bodenmodell
In diesem Bericht werden zwei Arten von Bodenmodellen verwendet: einheitlicher Boden und zweischichtiger Boden. SafeGrid kann jedoch auch mehrschichtige Böden modellieren. Siehe dazu den Artikel über die Leistung von Erdungsanlagen in mehrschichtigen Böden.
Die genaue Modellierung eines Erdungssystems erfordert die Verwendung eines zweischichtigen Bodenmodells. Der Grund dafür ist, dass der Bodenwiderstand, das Stufen- und das Berührungspotenzial von den oberen und unteren Bodenschichten abhängen.
Das Zweischichtenmodell besteht aus einer oberen Schicht des spezifischen Widerstands ρ1 mit endlicher Dicke und einer unteren Schicht des spezifischen Widerstands ρ2 mit unendlicher Tiefe.
Laut IEEE Std 80 ist die Darstellung eines Erdungsleiters auf der Grundlage eines äquivalenten zweischichtigen Erdungsmodells für die Auslegung eines sicheren Erdungssystems ausreichend.
| Beschreibung | Reflexionsfaktor, K1 | Spezifischer Widerstand der oberen Schicht, ρ1 (Ω.m) | Widerstand der untersten Schicht, ρ2 (Ω.m) |
|---|---|---|---|
| Uniform | 0 | 100 | 100 |
| Niedrig auf hoch | 0.9 | 100 | 1900 |
| 0.5 | 100 | 300 | |
| Hoch auf niedrig | -0.9 | 100 | 5.26 |
| -0.5 | 100 | 33.33 |
1 Reflexionsfaktor, K = (ρ2 - ρ1)/ (ρ2 + ρ1)
Analysierte Netzfälle
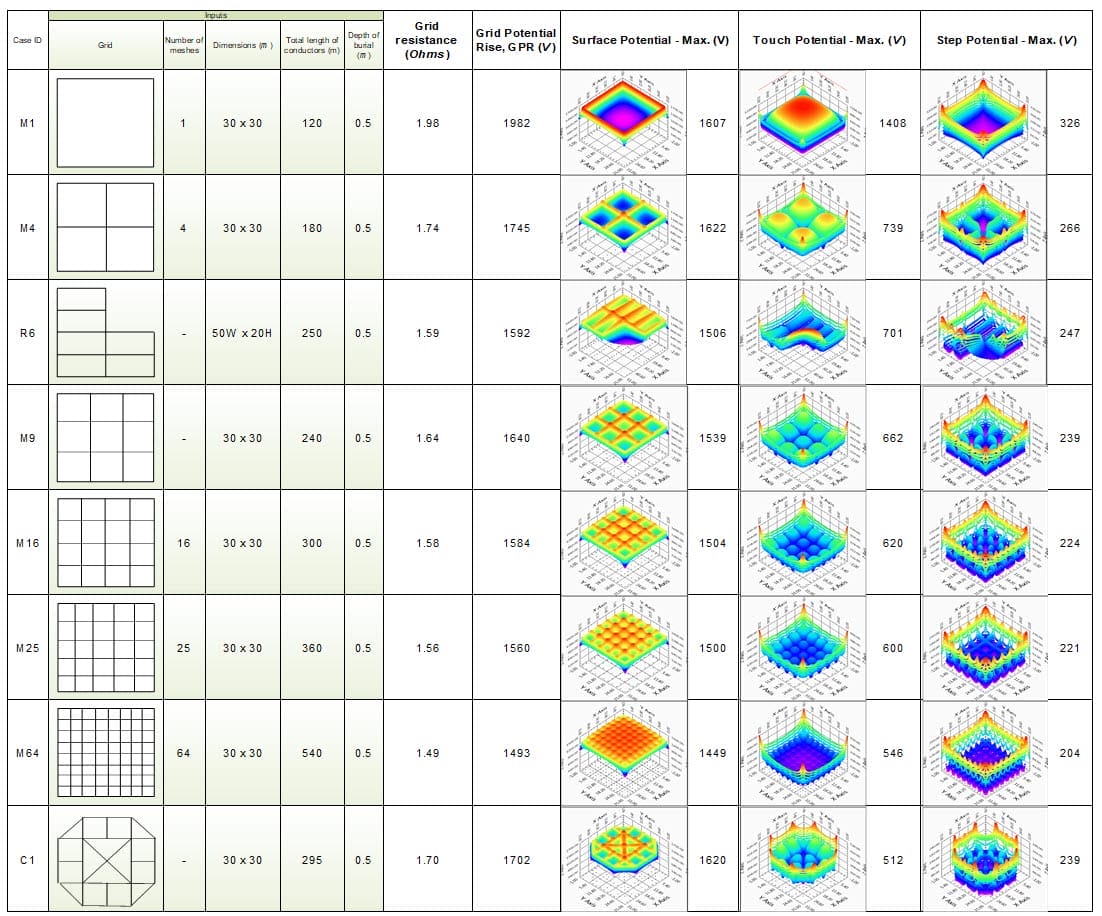
Die in Tabelle 2 dargestellten einfachen Erdungsnetze wurden im Detail analysiert.
SafeGrid kann jede beliebige Erdungsleiterkonfiguration modellieren.
Diese Erdungsnetze bestanden im Allgemeinen aus quadratischen oder rechteckigen Gittern mit Maschen, die gleichmäßig verteilte und gleich lange Leiter enthielten.
Die Vergrabungstiefe der Erdgitter wurde zwischen 0,01 m und 100 m variiert. Bei zweischichtigen Bodenmodellen wurde die Tiefe der obersten Schicht zwischen 0,1 m und 100 m variiert.
Die in Tabelle 2 aufgeführten Werte der Berechnungsergebnisse gelten für feste Parameterwerte wie angegeben. Diese Parameter wurden für dieselben einfachen Gitter während der parametrischen Analyse variiert.
Ergebnisse
Oberflächen-, Berührungs- und Stufenpotentiale
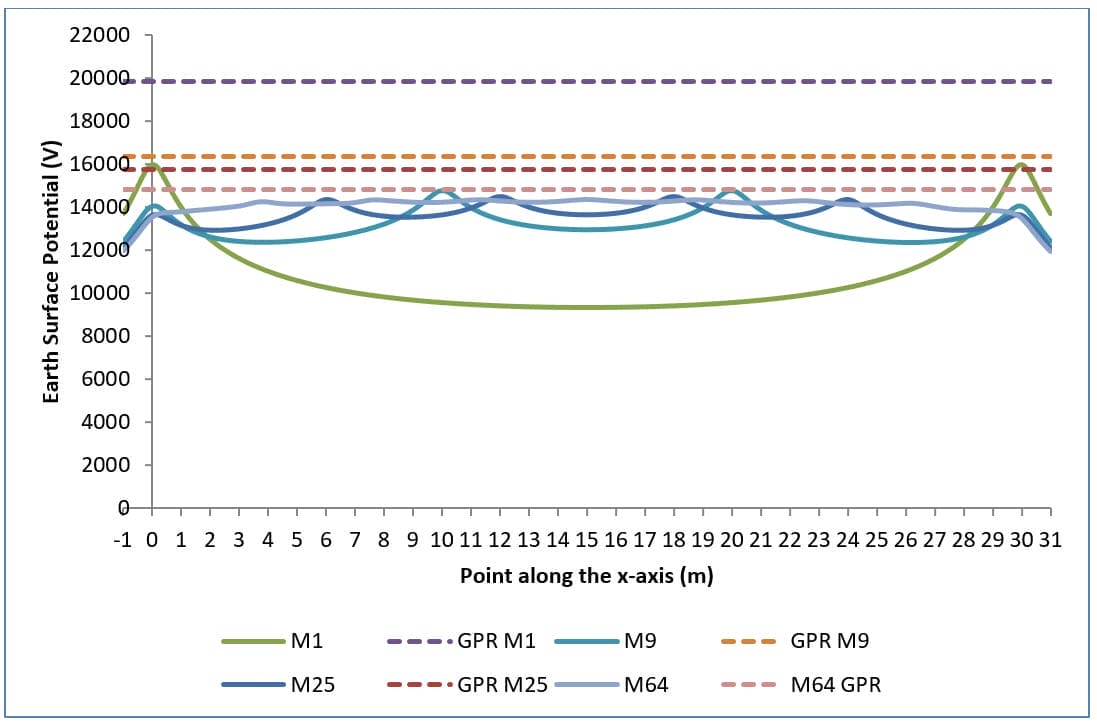
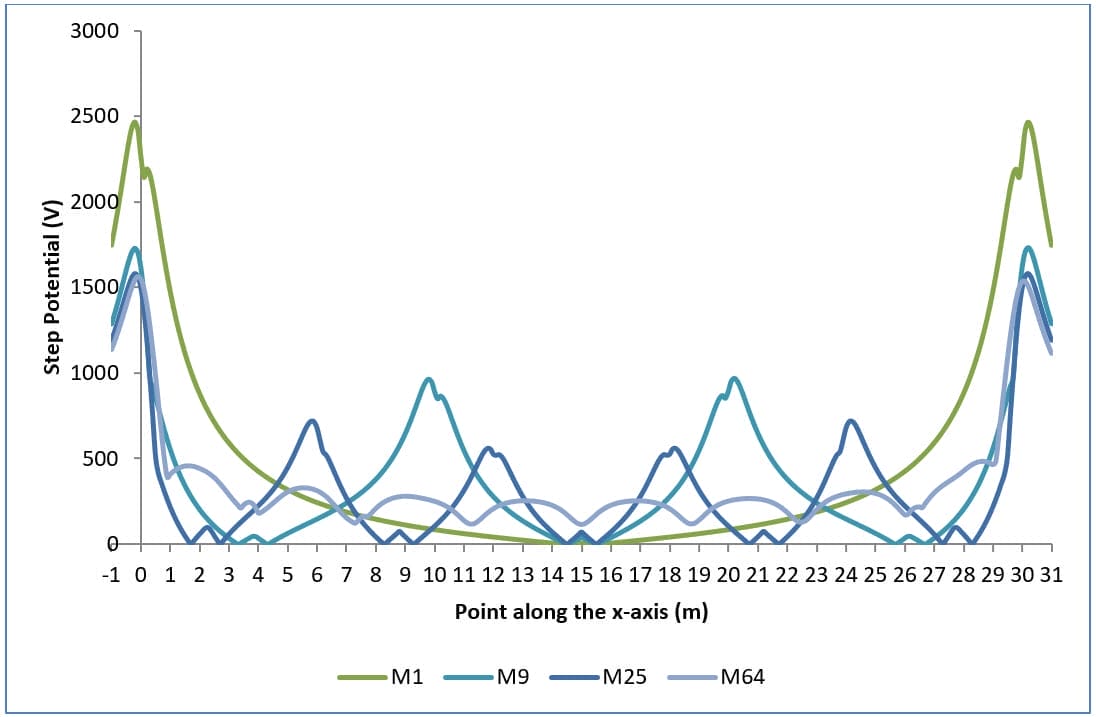
Die Abbildungen 1, 2 und 3 zeigen die Erdoberflächenpotentiale, Berührungspotentiale und Stufenpotentiale für verschiedene Gitterkonfigurationen.
Die Erhöhung der Anzahl der Leiter (oder Maschen) hat folgende Auswirkungen:
- Verringert den Netzwiderstand (R).
- Verringert den Netzpotentialanstieg (GPR), da GPR = R * Fehlerstrom.
- Das maximale Potential der Erdoberfläche nimmt ab.
- Die Berührungspotenziale sind reduziert (Abbildung 2).
- Die schlechtesten Berührungspotentiale bewegen sich zum Rand des Gitters hin. Dies wird durch die zunehmende Konkavität der Kurven in Abbildung 2 bei steigender Maschenzahl deutlich.
Diese letzte Bemerkung gilt für einen einheitlichen Boden, einen positiven Reflexionsfaktor K und gleichmäßig verteilte Gitterleiter. Andernfalls ist es schwierig, die Lage der ungünstigsten Berührungspotentiale vorherzusagen.

Stromdichte entlang von Leitern
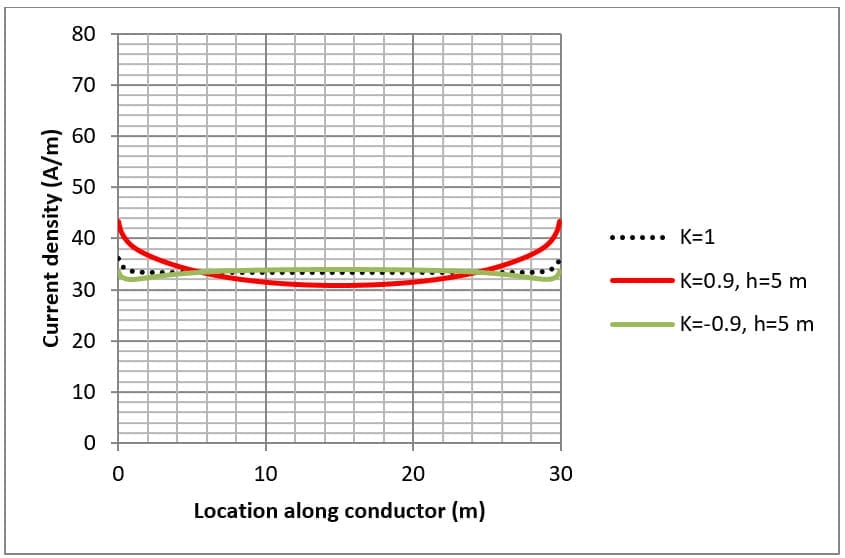
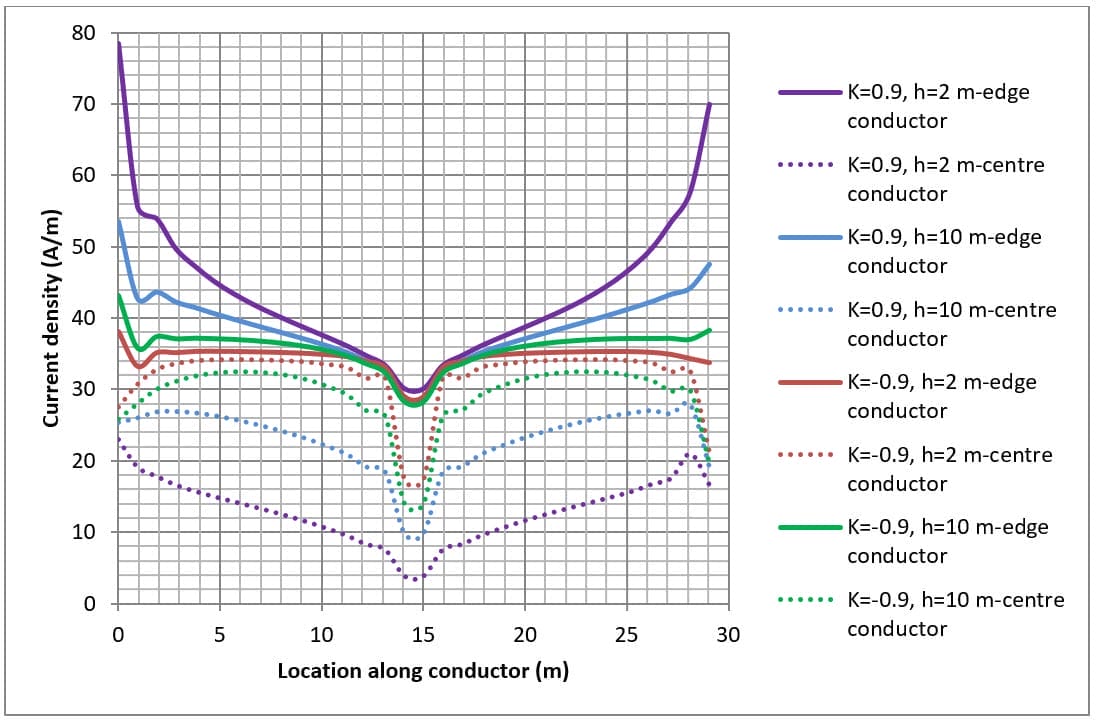
Die Stromdichte für Leiter ist in den Abbildungen 4, 5 und 6 für verschiedene Gitteranordnungen und Bodenwiderstandsstrukturen dargestellt.
Der angewandte Netzfehlerstrom hängt von der Gesamtlänge der Netzleiter für eine bestimmte Anordnung ab, wobei 1000 A für jeweils 30 Meter Leiter angewandt werden. Für ein einzelnes Netz, das aus 4 x 30 m langen Leitern besteht, beträgt der angewandte Fehlerstrom beispielsweise 4 x 1000 A.
Die Stromdichteverteilung entlang der Netzleiter ist nicht gleichmäßig, sondern eine komplexe Funktion, die je nach dem variiert:
- Gitteranordnung (d. h. die Anzahl der Maschen usw.)
- Lage des Leiters im Verhältnis zu anderen Leitern; und
- Struktur des Bodenwiderstandes
Wenn der Bodenwiderstand der oberen Schicht niedriger ist als der der unteren Schicht (d. h. K>0), konzentriert sich die Stromdichte auf die Enden der Leiter. Dies liegt daran, dass der Strom in der obersten Bodenschicht verbleibt und sich beim Abfließen in den Boden ausbreitet.
When the lower layer soil resistivity is higher than the top layer (i.e. K<0) the current density at the centre of the conductors can be just as high as at the ends. This is because the fault current escapes directly downwards toward the lower resistivity bottom layer.
Die Stromdissipation von Leitern entlang des Randes ist höher (durchgezogene Linien in Abbildung 5 und Abbildung 6) als bei Leitern in der Mitte (gestrichelte Linien in Abbildung 5 und Abbildung 6) des erdverlegten Erdnetzes.

Einfluss der obersten Bodenschicht auf den Gitterwiderstand
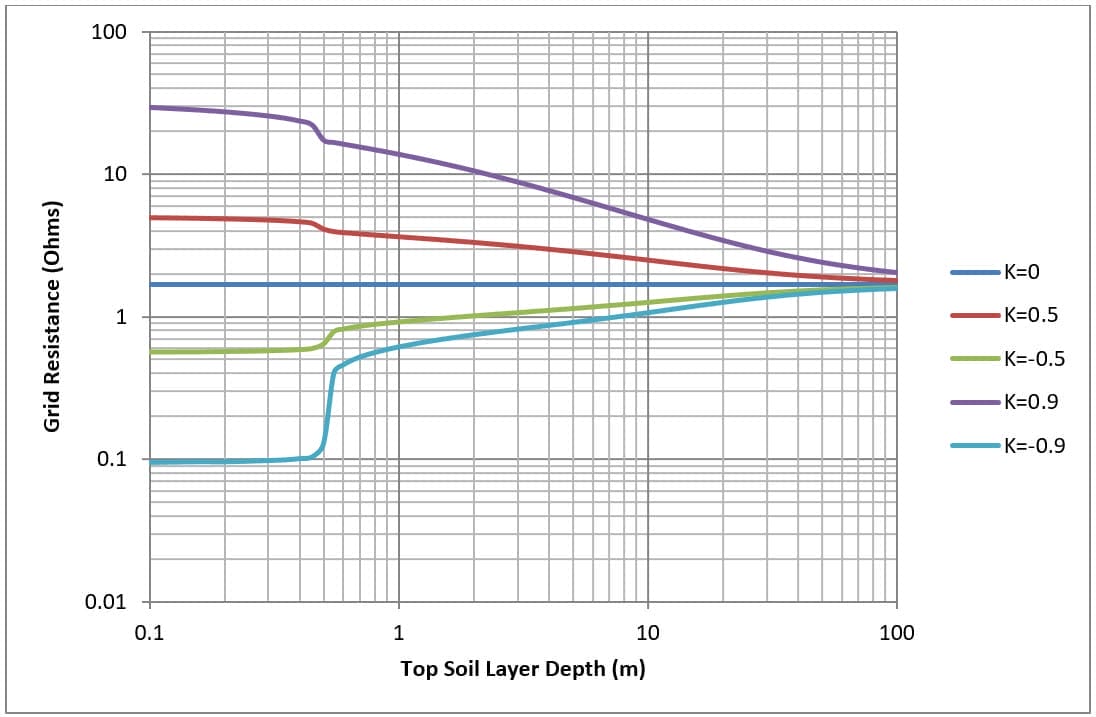
Abbildung 7 und Abbildung 8 zeigen für ein einfaches 30 x 30 Meter großes Netz (M4 und M16), das in 0,5 Metern Tiefe vergraben wurde, wie der Netzwiderstand mit der Dicke der obersten Bodenschicht variiert.
Der Bodenwiderstand der obersten Schicht ist fest, während der Widerstand der unteren Bodenschicht variiert wird, um unterschiedliche Reflexionsfaktoren (K) zu erhalten. Der Gitterwiderstand wird für unterschiedliche Tiefen der obersten Bodenschicht berechnet.
Die Änderung der Tiefe der obersten Bodenschicht hat folgende Auswirkungen:
- Bei einem einheitlichen Bodenmodell (Kontrollfall) gibt es keine Auswirkungen auf den Netzwiderstand.
- Für das Modell mit niedrigem auf hohem Boden (K>0) nimmt der Netzwiderstand mit zunehmender Tiefe der obersten Bodenschicht ab.
- For high on low soil model (K<0) as the depth of the top soil layer is increased grid resistance goes up.
- Wenn sich die Tiefe der obersten Schicht dem Unendlichen nähert, konvergiert der Gitterwiderstand mit dem einheitlichen Bodenmodell.
Man beachte die abrupte Änderung des Gitterwiderstands in allen Fällen bei einer Tiefe der obersten Bodenschicht von 0,5 m (was der Vergrabungstiefe des Gitters entspricht).
Es zeigt sich, dass der Gitterwiderstand durch die untere Bodenschicht beeinflusst wird, insbesondere bei Bodenschichten mit hohem Widerstand (K>0). Der Einfluss der unteren Bodenschicht auf den Gitterwiderstand kann bei großen Tiefen (etwa das Zwei- oder Mehrfache des gesamten Gitterdurchmessers) vernachlässigt werden.
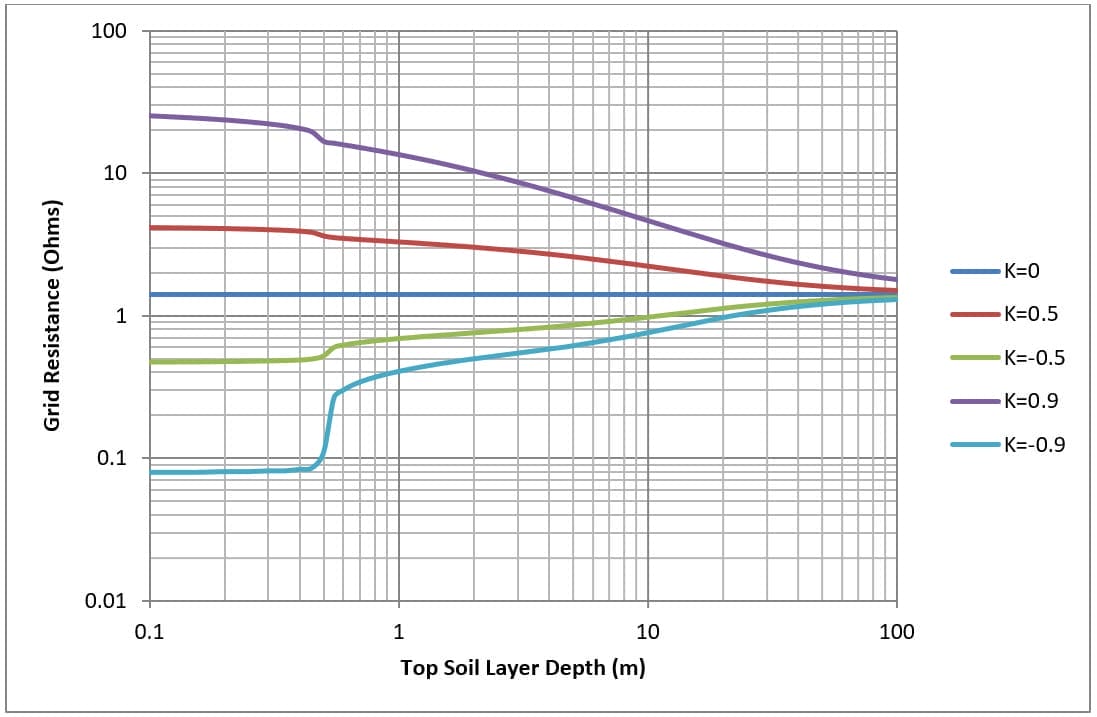
Auswirkung der Verlegetiefe des Netzes auf den Netzwiderstand
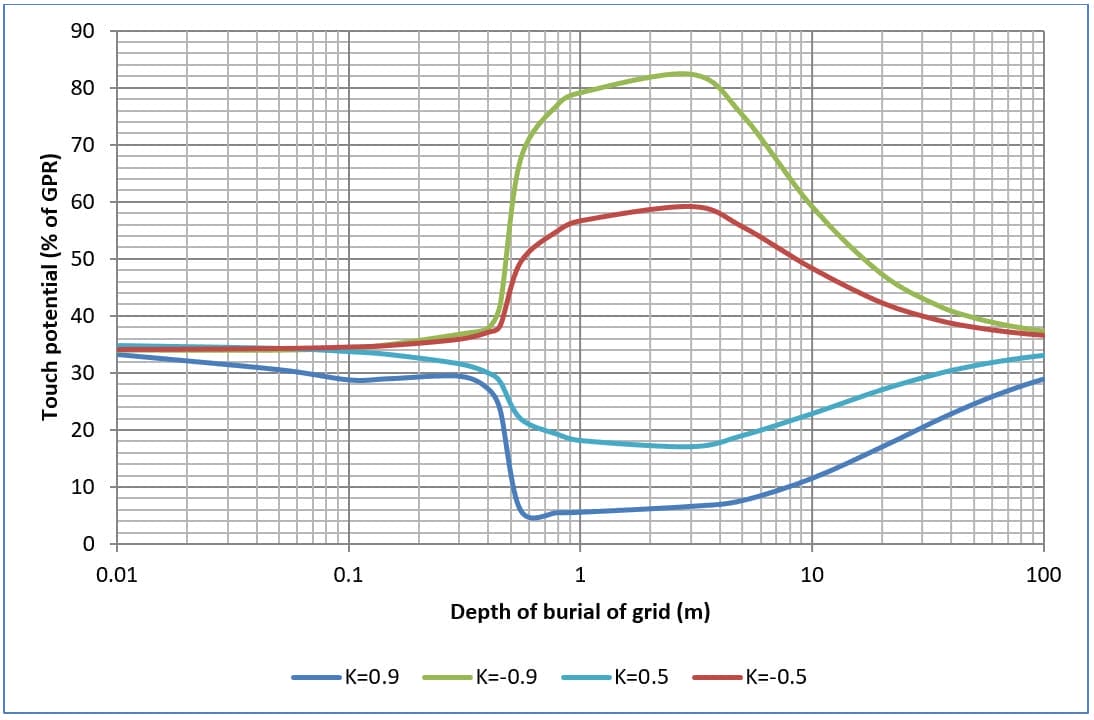
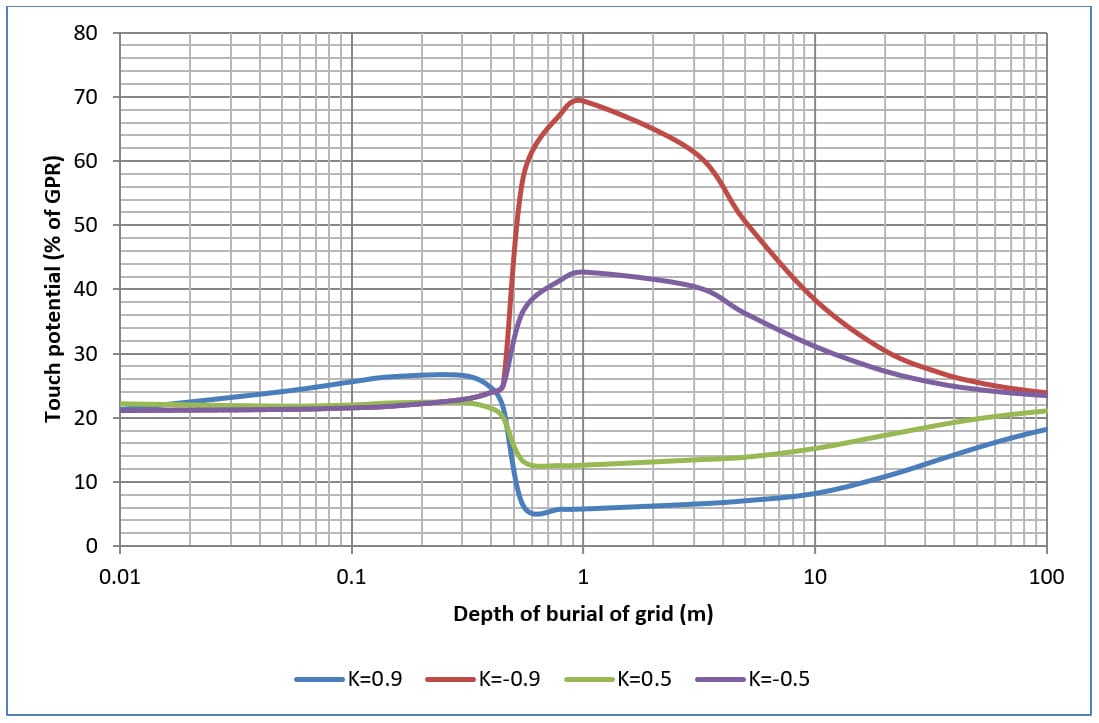
Die Abbildungen 9, 10, 11 und 12 zeigen die Auswirkungen auf die Berührungs- und Stufenpotentiale bei Änderung der Verlegetiefe von vier und sechzehn Maschengittern in zweischichtigem Boden.
Im Allgemeinen steigen mit zunehmender Verschüttungstiefe sowohl die Berührungs- als auch die Stufenpotentiale bis zu einem Maximalwert an und fallen dann wieder ab.
Die maximalen Berührungspotenziale treten auf, wenn der spezifische Bodenwiderstand der oberen Schicht deutlich größer ist als der der unteren Schicht (d. h. wenn K=-0,9).
Das maximale Berührungspotenzial verringert sich mit zunehmender Anzahl der Gittermaschen.


Schlussfolgerungen
Die genaue Bestimmung der Leistung von Erdungsnetzen ist für die Bereitstellung sicherer, funktioneller und wirtschaftlicher Konstruktionen von entscheidender Bedeutung.
Es hat sich gezeigt, dass die folgenden Parameter das Verhalten von Erdungsanlagen unter Fehlerbedingungen erheblich beeinflussen:
- Konfiguration des Erdungsnetzes.
- Bodenwiderstandseigenschaften.
- Vergrabungstiefe des Erdungsnetzes.
Diese Parameter wirken sich direkt auf die Leiterstromdichte (Ableitung in die Erde) aus, die sich auf den Netzpotentialanstieg (GPR), den Netzwiderstand, das Berührungspotential und das Stufenpotential auswirkt.
Der Zugang zu aufschlussreichen Software-Tools führt zu einer optimalen und sicheren Auslegung von Erdungsnetzen.
Referenzen
IEEE Guide for Safety in AC Substation Grounding, The Institute of Electrical and Electronics Engineers, Inc.
Dawalibi, F., Erdung von Übertragungsleitungen. EL-2699, Forschungsprojekt 1494-1. Montreal, Quebec, Kanada, Safe Engineering Services Ltd. 1.
Dawalibi, F. und Mukhedkar, D., "Parametrische Analyse von Erdungsnetzen". IEEE Transactions on Power Apparatus and Systems, Vol.PAS-98, No.5.
Kouteynikoff, P., "Numerische Berechnung des Erdungswiderstands von Umspannwerken und Türmen". IEEE Transactions on Power Apparatus and Systems, Vol.PAS-99, No.3.
Salama, M.M.A. et. al., "A formula for resistance of substation grounding grid in two-layer soil". IEEE Transactions on Power Delivery, Vol.10, No.3.