Was ist ein Spannungsabfall?
Der Spannungsabfall in einem Stromkreis ist die Differenz zwischen der Spannung an der Versorgungsseite und der Spannung an der Lastseite. Der Spannungsabfall hängt von der Stromlast, dem Kabeltyp und anderen Faktoren ab und hat einen erheblichen Einfluss auf die Mindestkabelgröße.
Die Normen legen Grenzwerte für den zulässigen prozentualen Spannungsabfall fest.
Gleichung für den Spannungsabfall
Zur Bestimmung des maximalen Spannungsabfalls kann eine Gleichung angewandt werden, die davon ausgeht, dass der Leistungsfaktor des Kabels gleich dem der Last ist.
Diese Gleichung kann wie folgt ausgedrückt werden:
\(V_d = I \cdot Z_c\) (Gl. 1)
Wo:
- Vdist der Spannungsabfall im Kabel, in Volt
- I ist der durch das Kabel fließende Strom in Ampere
- Zcist die Impedanz von Leitern in Ohm, wobei,= √((Rc2+Xc2))
Rc steht für den Kabelwiderstand, der eine Funktion des Leitermaterials, der Größe und der Betriebstemperatur ist. Xc steht für die Reaktanz des Kabels, die eine Funktion der Form und des Phasenabstands ist.
Beachten Sie, dass bei der Berechnung des Gleichspannungsabfalls der Wert für die Reaktanz Xcgleich Null ist.
Verwenden Sie den kostenlosen Spannungsabfall-Rechner für eine einfache und genaue Berechnung des Spannungsabfalls.
Spannungsabfall in Abhängigkeit vom Leistungsfaktor
Wenn sich die Versorgungsspannung und die Lastspannung hinsichtlich des Phasenwinkels unterscheiden, müssen andere Gleichungen verwendet werden, um diese Änderung auszugleichen. Wenn der Strom der Spannung vorauseilt, ist die Versorgungsspannung am Ende kleiner als die Lastspannung. Der Spannungsabfall IZc ist in allen Fällen des Leistungsfaktors identisch, unterscheidet sich jedoch hinsichtlich des Phasenwinkels, außer wenn die Leistungsfaktoren von Kabel und Last gleich sind, was bedeutet, dass der Spannungsabfall Vd ein Maximum von IZc ist. Die folgenden Gleichungen gelten für nacheilende Leistungsfaktoren.
Für ein einphasiges System
\(V_{d1\phi} = IL[2(R_c cos \theta + X_c sin \theta)]\) (Gl. 2)
Für ein symmetrisches Dreiphasensystem
\(V_{d3\phi} = IL[\sqrt{3}(R_c cos \theta + X_c sin \theta)]\) (Gl. 3)
Widerstandsfähigkeit und Betriebstemperatur des Kabels
Der Widerstand eines Kabels ist temperaturabhängig, und die Norm enthält Tabellen mit dem Widerstand für eine bestimmte Betriebstemperatur.
Liegt die Betriebstemperatur des Kabels unter dem in den Standardtabellen angegebenen Höchstwert, kann die Leitertemperatur anhand der folgenden Gleichung geschätzt werden:
Wo:
- I0 = Betriebsstrom, in Ampere
- IR = Bemessungsstrom gemäß den Strombemessungstabellen (aus den Tabellen 4-21 in AS/NZS 3008.1)
- 00= Betriebstemperatur des Kabels beim Transport, in Grad Celsius
- 0A= Temperatur der Umgebungsluft oder des Bodens, in Grad Celsius.
Sobald die Betriebstemperatur des Kabels berechnet ist, kann der Kabelwiderstand ausgewählt werden. Im Fall von AS/NZS 3008.1 enthalten die Tabellen 34-50 Widerstandswerte für die folgenden Betriebstemperaturen: 45oC, 60oC, 75oC, 80oC, 90oC, 110oC. Die berechnete Betriebstemperatur wird dann (konservativer) auf die nächstliegende Temperatur erhöht.
Spannungsabfall bei unsymmetrischen mehrphasigen Stromkreisen
In einem unsymmetrischen System fließt der Strom durch den Neutralleiter, wie im Phasendiagramm in Abbildung 1 dargestellt:
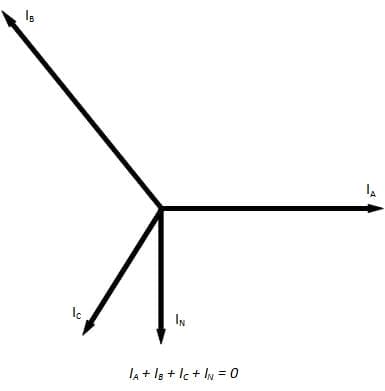
Es gibt zwei Möglichkeiten, den Spannungsabfall in diesen Fällen zu berücksichtigen. Eine konservative Lösung besteht darin, von einer ausgeglichenen dreiphasigen Last auszugehen und die Berechnungen anhand des Stroms durchzuführen, der in der am stärksten belasteten Phase fließt. Wenn jedoch nachgewiesen werden kann, dass die Ströme in den einzelnen Phasen über gleichbleibende Zeiträume hinweg unterschiedlich groß sind, kann der Spannungsabfall auf einphasiger Basis berechnet werden, indem der Spannungsabfall in der am stärksten belasteten Phase plus der Spannungsabfall im Neutralleiter addiert wird, wie in der folgenden Gleichung dargestellt.
Im nächsten Abschnitt werden wir ein Beispiel für die Berechnung des Spannungsabfalls geben.
Beispiel für die Berechnung des Spannungsabfalls
Einadrige Kabel mit Kupferleitern und XLPE-Isolierung sind an eine 3-phasige 400-V-Versorgung angeschlossen. Die Anlage ist direkt im Erdreich verlegt (die Referenz-Umgebungstemperatur beträgt 25oC) über 120 m Länge verlegt. Der Laststrom beträgt 240 A bei einem Leistungsfaktor von 0,9.
Wie hoch ist der dreiphasige Spannungsabfall?
Schritt 1: Bestimmung der Betriebstemperatur des Kabels
Abbildung 2: Darstellung des direkt in der Erde verlegten Kabels.
Die normale Betriebstemperatur für XLPE-isolierte Kabel beträgt 90˚C. Verwenden Sie Gleichung 4 für die Betriebstemperatur des Kabels:
\(\theta_0 = (90^{\circ} - 25^{\circ})(\frac{240}{277})^2 + 25^{\circ}\)
Schritt 2: Bestimmung des Kabelwiderstands auf der Grundlage der Betriebstemperatur des Kabels
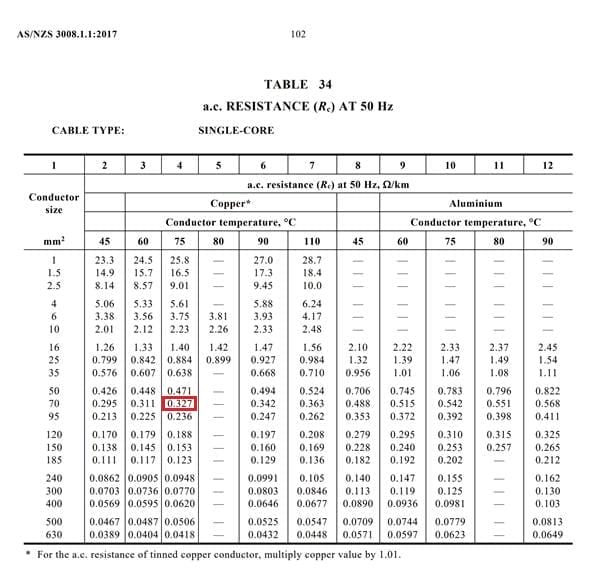
Anhand der Tabelle 34 (siehe Anhang 1) können wir den Wechselstromwiderstand des Kabels ermitteln, der der Leitergröße und der Leitertemperatur entspricht, die der in Schritt 1 berechneten Betriebstemperatur des Kabels am nächsten kommt. Da wir eine Temperatur von 73,8° berechnet haben, sollten wir die Temperatur aufrunden und davon ausgehen, dass 75° die genaueste Temperatur ist, die wir verwenden können.
Nach Tabelle 34 beträgt der Widerstand eines Kabels mit einem 70 mm2 großen Kupferleiter und einer Betriebstemperatur von 75° 0,327 Ω/km, oder 0,000327 Ω/m.
Schritt 3: Bestimmung der Kabelreaktanz
Der Blindwiderstand bei einadrigen Kabeln hängt vom Kabeltyp und der Trennung der Kabel ab.
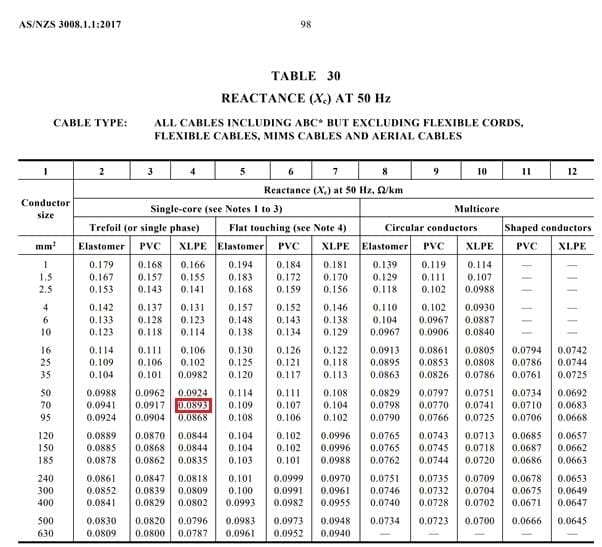
Mit Hilfe von Tabelle 30 (siehe Anlage 2) können wir den Blindwiderstand bei 50 Hz ermitteln.
Unsere Kabel sind dreifach gekreuzt, daher beträgt der Blindwiderstand des Kabels nach Spalte 3 0,0893 Ω/km oder 0,0000893 Ω/m.
Schritt 4: Berechnung des Spannungsabfalls anhand des Leistungsfaktors und der Betriebstemperatur des Kabels
Wir werden Gleichung 3 verwenden, um den dreiphasigen Spannungsabfall zu berechnen. Dazu benötigen wir den Phasenwinkel der Last auf der Grundlage des gegebenen Lastleistungsfaktors wie folgt:
\(\theta = cos^{-1}(0.9)\)
\(\theta = 25.84193276^{\circ} = 0.4510268 \; rads\)
\(sin\theta = 0.43588989\)
Jetzt haben wir alle Parameter, die wir zur Berechnung des dreiphasigen Spannungsabfalls benötigen:
\(V_{d3\phi} = 250 \cdot 120[\sqrt{3}(0,000327 \cdot 0,9 + 0,0000893 \cdot 0,43588989)]\)
\(V_{d3\phi} = 17.315 \; V\)
Der Spannungsabfall in Prozent der Versorgungsspannung beträgt 17,315 / 400 V, also 4,33 %.
Anhänge
Anhang 1 - Tabelle 34 mit rot hervorgehobenem Wert
Anhang 2 - Tabelle 30 mit rot hervorgehobenem Wert