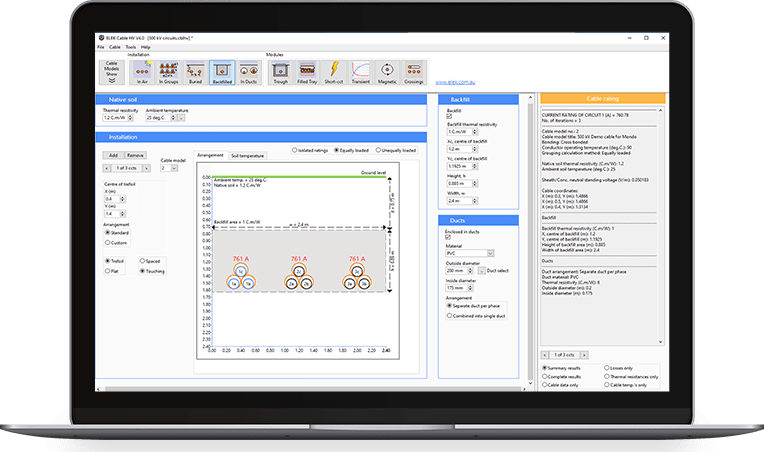
Wie hoch ist der Ladestrom im Kabel?
Der Ladestrom ist definiert als der Strom, der durch die Shunt-Kapazität einer Übertragungsleitung fließt und sowohl bei Erdkabeln als auch bei Freileitungen auftritt. Die Shunt-Kapazität und damit die Ladeströme sind bei Erdkabeln 10-20 mal größer als bei Freileitungen. Beachten Sie, dass die Serieninduktivität bei Freileitungen 2-3 mal größer ist als bei Erdkabeln [1].
Der Ladestrom steigt linear mit der Kabellänge und auch mit der Spannungshöhe und wird zu einem wichtigen Faktor für lange Kabelübertragungen; in der Regel 40 km oder länger für Übertragungsspannungen unter 220 kV und 20 km oder länger für Übertragungsspannungen von 220 kV oder mehr [2].
Der Ladestrom hat zur Folge, dass der an der Quelle eingespeiste Strom höher sein muss, um die Kabelkapazität auszugleichen, damit die aktive Last versorgt werden kann. Der Ladestrom erzeugt Wärmeverluste im Kabel, die bei langen Übertragungsleitungen so hoch sein können wie die Wärmeleistung des Kabels.
Beachten Sie, dass das Phänomen des Ladestroms und die damit verbundene Begrenzung der maximalen Leitungslänge nur für Wechselstromkabel gilt. Im Gegensatz zu Wechselstromkabeln führt das Fehlen des Ladestroms bei Gleichstromkabeln zu praktisch unbegrenzten Übertragungsstrecken über Gleichstrom.
Gleichungen für den Ladestrom
Die Gleichung für den Ladestrom (für Wechselstromkabel) kann wie folgt ausgedrückt werden:

- C = Kapazität pro Längeneinheit (μF/km)
- ω = Winkelfrequenz der Spannung (s-1)
- U = RMS-Netzspannung (Phase zu Phase) (kV)
- L = Länge (km)
- IC = Ladestrom (A)
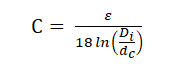
- ε = relative Dielektrizitätskonstante der Isolierung ( = 2,5 bei XLPE)
- Di = Außendurchmesser der Isolierung (ohne Schirm) (mm)
- dC = Durchmesser des Leiters einschließlich Abschirmung, falls vorhanden (mm)
Kritische Länge der Kabel
Mit zunehmender Kabellänge sinkt der an die Last abgegebene Strom aufgrund des steigenden Ladestroms. Die Länge, bei der der Ladestrom gleich dem Versorgungsstrom wird, wird als kritische Länge definiert, und an diesem Punkt ist der Ladestrom für alle Wärmeverluste im Kabel verantwortlich. Die Gleichung für die kritische Länge lautet:

- LC = Kritische Länge (km)
- IS = Nennversorgungsstrom von der Quelle oder vom Sender (A)
- U = RMS-Netzspannung (Phase zu Phase) (kV)
Berechnung der von der Last aufgenommenen Wirkleistung
Die maximale übertragene Leistung, die bei einer unterirdischen Radialverbindung am Lastpunkt ankommt, hängt von der Netzfrequenz und -spannung, der Kabellänge, der Spannung über der Isolierung und der Kabelkapazität ab [1]. Zur Berechnung der gesamten an der Last empfangenen Wirkleistung auf der Grundlage der Länge der Übertragungsleitung kann die folgende Gleichung verwendet werden:
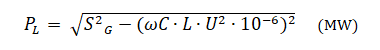
Wo:
- PL = Wirkleistung (at ) am Lastpunkt
- SG = Einspeiseleistung an der Quelle (MVA)
- L = Länge der unterirdischen Verbindung (km)
Die Scheinleistung SG an der Quelle kann wie folgt berechnet werden, wobei eine 3-Phasen-Konfiguration angenommen wird:
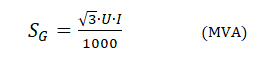
Wo:
- PL = Wirkleistung (at ) am Lastpunkt
- SG = Einspeiseleistung an der Quelle (MVA)
- L = Länge der unterirdischen Verbindung (km)
Die Scheinleistung SG an der Quelle kann wie folgt berechnet werden, wobei eine 3-Phasen-Konfiguration angenommen wird:
Kompensation des Ladestroms
Um den kapazitiven Blindwiderstand des Kabels zu kompensieren, werden induktive Nebenschlussdrosseln eingesetzt. Dies ist normalerweise bei langen Kabelstrecken erforderlich. Eine Faustregel besagt, dass eine Kompensation in Betracht zu ziehen ist, wenn die übertragbare Wirkleistung um etwa 15 % gesunken ist [3].
Bei der Bemessung der Drosseln muss berücksichtigt werden, ob das Kabelsystem in der Lage ist, Spannungseinbrüche im Leerlauf zu verkraften und den Ladestrom bei Volllast zu kompensieren. Nebenschlussdrosseln können in regelmäßigen Abständen angeordnet werden, aber diese Anordnung kann sich als kostspielig erweisen, weshalb eine gründliche Systemanalyse für eine optimale Leistung erforderlich ist. Es kann eine einfache Formel angewendet werden, die den Blindleistungsbedarf von Erdkabeln zusammenfasst [1]. Es ist zu beachten, dass diese Gleichungen nur einen grundlegenden Hinweis auf die Kabelkompensation geben und für eine vorläufige Netzstudie verwendet werden sollten.
Ein Näherungswert für den Induktivitätswert kann mit einer einfachen Formel wie unten dargestellt abgeleitet werden:
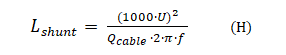
- Höchstwahrscheinlich werden die Gleichungen (6) und (7), wie in der E-Mail erwähnt, entfernt.
Wo
- Lshunt= Shunt-Induktivität (H)
- Qcable = Kabel-Blindleistung (VAR)
- CT = Gesamtkapazität des Kabels über die gesamte Übertragungslänge (F)
Prüfung der kritischen Länge
Beispiel 1 - 132-kV- und 22-kV-Kabel, beide mit 531 A belastet
Abbildung 1 zeigt einen Vergleichstest mit einem 132-kV-Kabel und einem 22-kV-Kabel. Jedes Kabel liefert 20,23 MW bei einer Spannung von 22 kV und führt einen Strom von 531 A. Durch die Verwendung eines Kabels mit höherer Nennspannung verlängert sich die kritische Länge aufgrund der niedrigeren Kapazitätswerte weiter. Die geringere Kapazität ist auf die größere Isolationsdicke der Kabel zurückzuführen und kann anhand von (2) berechnet werden.
Wie aus Abbildung 1 ersichtlich ist, ist das 132-kV-Kabel bei gleicher Wirkleistung 928 km länger als das 22-kV-Kabel mit nur 386 km. Bei der 386-km-Marke beträgt die Wirkleistung des 132-kV-Kabels 18,4 MW. Dies entspricht einem Rückgang von nur 9 % gegenüber der Nennleistung, so dass ein Kabel mit einer höheren Spannung verwendet werden könnte, um die Energieeffizienz für die vom Planer vorgesehene Übertragungslänge zu verbessern.
Beispiel 2 - Einadrige 132-kV-Kabel verschiedener Größen
Abbildung 2 zeigt einen Vergleichstest mit einem einadrigen 132-kV-Kabel in drei verschiedenen Größen - 300 mm2, 630 mm2 und 1200 mm2. Jedes der Kabel mit unterschiedlichem Querschnitt liefert eine Leistung von 121,4 MW bei einer Spannung von 132 kV und einem Strom von 531 A. Die Kabel in jedem Stromkreis berühren sich, sind dreifach verlegt und 0,5 m unter der Erde vergraben. Mit zunehmendem Leiterdurchmesser nimmt die kritische Länge ab. Obwohl die Isolationsdicke bei allen Kabeln gleich bleibt, nimmt die Kapazität durch die Vergrößerung der Leiter zu.
Beispiel 3 - Erdverlegte 132-kV-Kabel bei 50 Hz und 60 Hz
Abbildung 3 zeigt zwei Diagramme mit unterschiedlichen Systemfrequenzen, wobei beide Stromkreise mit 132 kV bemessen sind, in 0,5 m Tiefe vergraben sind, sich berühren und mit einer Querschnittsfläche von 300 mm2 dreifach angeordnet sind. Die 60-Hz-Darstellung (grün) hat eine kürzere kritische Länge als die 50-Hz-Darstellung (blau). Mit steigender Frequenz nimmt die kritische Länge ab, wie aus (3) ersichtlich ist.
Referenzen:
- CIGRE, "General Guidelines for the Integration of a New Underground Cable System in the Network - Working Group B1.19", CIGRE, 2004. Abgerufen am: Sep. 12, 2020. [Online]. Verfügbar unter: https://e-cigre.org/publication/250-technical-and-environmental-issues-regarding-the-integration-of-a-new-hv-underground-cable-system-in-the-network.
- CIGRE, "Implementation of Long AC HV and EHV Cable Systems - Working Group B1.47", CIGRE, 2017. Accessed on: Sep. 14, 2020. [Online]. Verfügbar unter: https://e-cigre.org/publication/680-implementation-of-long-ac-hv-and-ehv-cable-systems.
- CIGRE, "A Guide for Rating Calculations of Insulated Cables - Working Group B1.35", CIGRE, 2015. Accessed on: Sep. 12, 2020. [Online]. Verfügbar unter: https://e-cigre.org/publication/640-a-guide-for-rating-calculations-of-insulated-cables.
- Elektrische Leitungen - Berechnung der Strombelastbarkeit - Teil 1-1: Gleichungen für die Strombelastbarkeit (100% Lastfaktor) und Berechnung der Verluste - Allgemeines, IEC 60287-1-1:2014
- Kabel-Hochspannungs-Software Version 4.3 (2021). Elektrotechnik.
Testen Sie kostenlos unsere Berechnungssoftware für Hochspannungskabel nach IEC 60287.