Che cos'è la caduta di tensione?
La caduta di tensione in un circuito rappresenta la differenza tra la tensione all'estremità dell'alimentazione e la tensione all'estremità del carico. La caduta di tensione dipende dal carico di corrente, dal tipo di cavo e da altri fattori e ha un impatto significativo sulle dimensioni minime del cavo.
Gli standard stabiliscono i limiti percentuali di caduta di tensione consentiti.
Equazione della caduta di tensione
Per determinare la caduta di tensione massima, è possibile applicare un'equazione nell'ipotesi che il fattore di potenza del cavo sia uguale a quello del carico.
Questa equazione può essere espressa come:
\(V_d = I \cdot Z_c\) (Eq. 1)
Dove:
- Vdè la caduta di tensione nel cavo, in volt
- I è la corrente che attraversa il cavo, espressa in ampere.
- Zcè l'impedenza dei conduttori in ohm per cui,= √((Rc2+Xc2))
Rc rappresenta la resistenza del cavo, che è funzione del materiale del conduttore, delle dimensioni e della temperatura di esercizio. Xc rappresenta la reattanza del cavo in funzione della forma e della distanza di fase.
Per i calcoli della caduta di tensione CC, il valore della reattanza Xcè zero.
Utilizzate il calcolatore di caduta di tensione gratuito per calcolare in modo semplice e preciso la caduta di tensione.
Caduta di tensione in base al fattore di potenza
Nel caso in cui le tensioni di alimentazione e di carico differiscano in termini di angolo di fase, è necessario utilizzare un'altra serie di equazioni per compensare questa variazione. Quando la corrente è in testa alla tensione, la tensione di alimentazione finisce per essere più piccola della tensione di carico. La caduta di tensione IZc è identica in tutti i casi di fattore di potenza, ma è diversa in termini di angolo di fase, ad eccezione del caso in cui i fattori di potenza del cavo e del carico sono uguali, in cui la caduta di tensione Vd è il massimo di IZc. Le seguenti equazioni si applicano ai fattori di potenza in ritardo.
Per un sistema monofase
\(V_{d1\phi} = IL[2(R_c cos \theta + X_c sin \theta)]\) (Eq. 2)
Per un sistema trifase bilanciato
\(V_{d3\phi} = IL[\sqrt{3}(R_c cos \theta + X_c sin \theta)]\) (Eq. 3)
Resistenza e temperatura di esercizio del cavo
La resistenza di un cavo dipende dalla temperatura e lo standard fornisce tabelle di resistenza per una particolare temperatura di esercizio.
In una situazione in cui la temperatura di esercizio del cavo è inferiore al valore massimo previsto dalle tabelle standard, la temperatura del conduttore può essere stimata utilizzando la seguente equazione:
Dove:
- I0 = corrente di esercizio, in ampere
- IR = corrente nominale prevista dalle tabelle di corrente nominale (dalle tabelle 4-21 di AS/NZS 3008.1)
- 00= temperatura di esercizio del cavo durante il trasporto, in gradi Celsius
- 0A= temperatura ambiente dell'aria o del suolo, in gradi Celsius.
Una volta calcolata la temperatura di esercizio del cavo, è possibile selezionare la resistenza del cavo. Nel caso di AS/NZS 3008.1, le tabelle 34-50 forniscono i valori di resistenza per le seguenti temperature di esercizio 45oC, 60oC, 75oC, 80oC, 90oC, 110oCe la temperatura di esercizio calcolata viene aumentata (in modo più conservativo) alla temperatura più vicina.
Caduta di tensione per circuiti multifase sbilanciati
In un sistema sbilanciato, la corrente fluisce attraverso il conduttore di neutro, come illustrato dal diagramma dei fasori nella Figura 1:
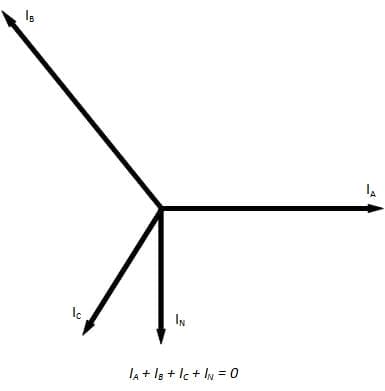
In questi casi esistono due modi di trattare la caduta di tensione. Una soluzione conservativa consiste nell'ipotizzare un carico trifase bilanciato e nell'eseguire i calcoli utilizzando la corrente che scorre nella fase più carica. Tuttavia, se è possibile dimostrare che le correnti in ciascuna fase sono di entità diversa per periodi coerenti, la caduta di tensione può essere calcolata su base monofase sommando la caduta di tensione nella fase più carica e la caduta di tensione nel neutro, come mostrato dall'equazione seguente.
Nella prossima sezione verrà presentato un esempio di calcolo della caduta di tensione.
Esempio di calcolo della caduta di tensione
I cavi unipolari con conduttori in rame e isolamento in XLPE sono collegati a un'alimentazione trifase a 400 V. L'installazione è interrata direttamente nel terreno (la temperatura ambiente di riferimento è di 25oC) su una lunghezza di 120 m. La corrente di carico è di 240 A con fattore di potenza 0,9.
Qual è la caduta di tensione trifase?
Passo 1: determinare la temperatura di esercizio del cavo
Figura 2: Illustrazione del cavo interrato direttamente nel terreno.
La temperatura di esercizio normale per i cavi isolati in XLPE è di 90˚C. Utilizzando l'equazione 4 per la temperatura di esercizio dei cavi:
\(\theta_0 = (90^{\circ} - 25^{\circ})(\frac{240}{277})^2 + 25^{\circ}})
Fase 2: Determinazione della resistenza del cavo in base alla sua temperatura di esercizio
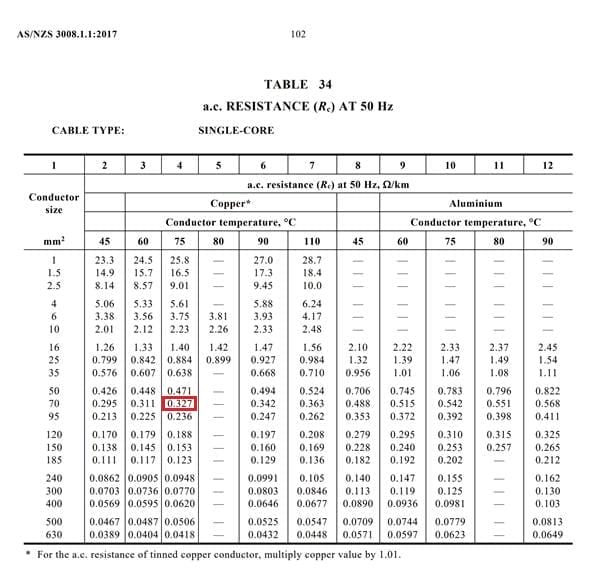
Utilizzando la Tabella 34 (fare riferimento all'Appendice 1), possiamo trovare la resistenza CA del cavo corrispondente alla dimensione del conduttore e alla temperatura del conduttore più vicina alla temperatura di esercizio del cavo calcolata al punto 1. Poiché abbiamo calcolato una temperatura di 73,8°, dobbiamo arrotondare per eccesso e ritenere che 75° sia la temperatura più accurata da utilizzare. Poiché abbiamo calcolato una temperatura di 73,8°, dovremmo arrotondare la temperatura per eccesso e ritenere che 75° sia la temperatura più accurata da utilizzare.
Secondo la Tabella 34, la resistenza di un cavo con un conduttore di rame da 70 mm2 e una temperatura di esercizio di 75° è di 0,327 Ω/km, ovvero 0,000327 Ω/m.
Fase 3: determinazione della reattanza del cavo
La reattanza per i cavi unipolari dipende dal tipo di cavo e dalla separazione dei cavi.
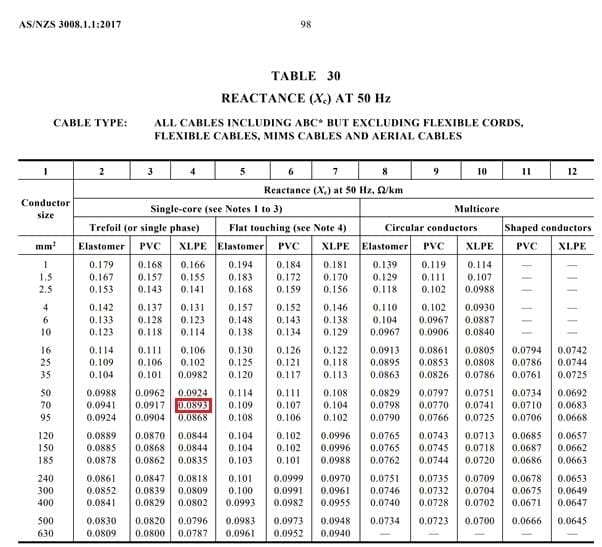
Utilizzando la Tabella 30 (fare riferimento all'Appendice 2) si può trovare la reattanza a 50 Hz.
I nostri cavi sono disposti a trefoil, quindi dalla colonna 3 la reattanza del cavo è di 0,0893 Ω/km , ovvero 0,0000893 Ω/m.
Fase 4: Calcolo della caduta di tensione in base al fattore di potenza e alla temperatura di esercizio del cavo
Utilizzeremo l'equazione 3 per calcolare la caduta di tensione trifase. A tal fine, abbiamo bisogno dell'angolo di fase del carico in base al fattore di potenza del carico dato, come segue:
\(\theta = cos^{-1}(0.9)\)
\(\theta = 25.84193276^{\circ} = 0.4510268 \; rads\)
\(sin\theta = 0,43588989)
Ora abbiamo tutti i parametri necessari per calcolare la caduta di tensione trifase:
\(V_{d3\phi} = 250 \cdot 120[\sqrt{3}(0,000327 \cdot 0,9 + 0,0000893 \cdot 0,43588989)]\)
\(V_{d3\phi} = 17.315 \; V\)
La caduta di tensione in percentuale della tensione di alimentazione è 17,315 / 400 V, ovvero 4,33%.
Appendici
Appendice 1 - Tabella 34 con valore rilevante evidenziato in rosso
Appendice 2 - Tabella 30 con valore rilevante evidenziato in rosso