Qu'est-ce que la chute de tension ?
La chute de tension dans un circuit représente la différence entre la tension à l'extrémité de l'alimentation et la tension à l'extrémité de la charge. La chute de tension dépend de la charge actuelle, du type de câble et d'autres facteurs, et a un impact significatif sur la taille minimale du câble.
Les normes fixent des limites de chute de tension en pourcentage.
Équation de la chute de tension
Pour déterminer la chute de tension maximale, une équation peut être appliquée en supposant que le facteur de puissance du câble est égal à celui de la charge.
Cette équation peut être exprimée comme suit
\(V_d = I \cdot Z_c\) (Eq. 1)
Où ?
- Vdest la chute de tension dans le câble, en volts
- I est le courant circulant dans le câble en ampères
- Zcest l'impédance des conducteurs en ohms avec,= √((Rc2+Xc2))
Rc représente la résistance du câble qui est fonction du matériau du conducteur, de la taille et de la température de fonctionnement. Xc représente la réactance du câble qui est fonction de la forme et de l'espacement des phases.
Remarque : pour les calculs de chute de tension continue, la valeur de la réactance Xcest nulle.
Utilisez le calculateur de chute de tension gratuit pour calculer facilement et précisément la chute de tension.
Chute de tension en fonction du facteur de puissance
Dans le cas où les tensions d'alimentation et de charge diffèrent en termes d'angle de phase, une autre série d'équations doit être utilisée pour compenser ce changement. Lorsque le courant précède la tension, la tension d'alimentation finit par être inférieure à la tension de charge. La chute de tension IZc est identique dans tous les cas de facteur de puissance, mais elle est différente en termes d'angle de phase, sauf lorsque les facteurs de puissance du câble et de la charge sont égaux, ce qui montre que la chute de tension Vd est un maximum de IZc. Les équations suivantes s'appliquent aux facteurs de puissance décalés.
Pour un système monophasé
\(V_{d1\phi} = IL[2(R_c cos \theta + X_c sin \theta)]\) (Eq. 2)
Pour un système triphasé équilibré
\(V_{d3\phi} = IL[\sqrt{3}(R_c cos \theta + X_c sin \theta)]\) (Eq. 3)
Résistance et température de fonctionnement du câble
La résistance d'un câble dépend de la température et la norme fournit des tableaux de résistance pour une température de fonctionnement donnée.
Lorsque la température de fonctionnement du câble est inférieure à la valeur maximale indiquée dans les tableaux de la norme, la température du conducteur peut être estimée à l'aide de l'équation suivante :
Où ?
- I0 = courant de fonctionnement, en ampères
- IR = courant nominal indiqué dans les tableaux de courant nominal (tableaux 4-21 de la norme AS/NZS 3008.1)
- 00= Température de fonctionnement du câble en cours de transport, en degrés Celsius
- 0A= température ambiante de l'air ou du sol, en degrés Celsius.
Une fois que la température de fonctionnement du câble est calculée, la résistance du câble peut être sélectionnée. Dans le cas de la norme AS/NZS 3008.1, les tableaux 34-50 fournissent des valeurs de résistance pour les températures de fonctionnement suivantes : 45oC, 60oC, 75oC, 80oC, 90oC, 110oC. La température de fonctionnement calculée est ensuite augmentée (de manière plus conservatrice) à la température la plus proche.
Chute de tension pour les circuits multiphasés déséquilibrés
Dans un système déséquilibré, le courant passe par le conducteur neutre, comme l'illustre le diagramme de phase de la figure 1 :
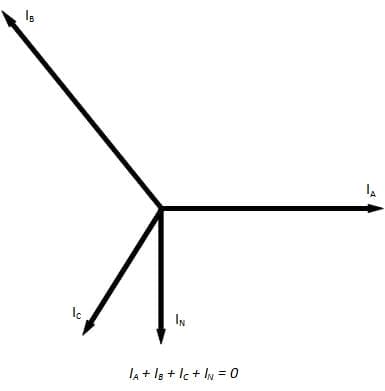
Il y a deux façons de traiter la chute de tension dans ces cas. Une solution conservatrice consiste à supposer une charge triphasée équilibrée et à effectuer les calculs en utilisant le courant circulant dans la phase la plus chargée. Toutefois, lorsqu'il peut être démontré que les courants dans chaque phase sont de magnitude différente pendant des périodes constantes, la chute de tension peut être calculée sur une base monophasée en additionnant la chute de tension dans la phase la plus chargée et la chute de tension dans le neutre, comme le montre l'équation ci-dessous.
Dans la section suivante, nous donnerons un exemple de calcul de la chute de tension.
Exemple de calcul de la chute de tension
Les câbles unipolaires à conducteurs en cuivre et à isolation XLPE sont raccordés à une alimentation triphasée de 400 V. L'installation est enterrée directement dans le sol (la température ambiante de référence est de 25oC) sur une longueur de 120 m. Le courant de charge est de 240 A avec un facteur de puissance de 0,9.
Quelle est la chute de tension triphasée ?
Étape 1 : Déterminer la température de fonctionnement du câble
Figure 2 : Illustration du câble enterré directement dans le sol.
La température de fonctionnement normale des câbles à isolation XLPE est de 90˚C. En utilisant l'équation 4 pour la température de fonctionnement du câble :
\(\theta_0 = (90^{\circ} - 25^{\circ})(\frac{240}{277})^2 + 25^{\circ}\)
Étape 2 : Déterminer la résistance du câble en fonction de sa température de fonctionnement
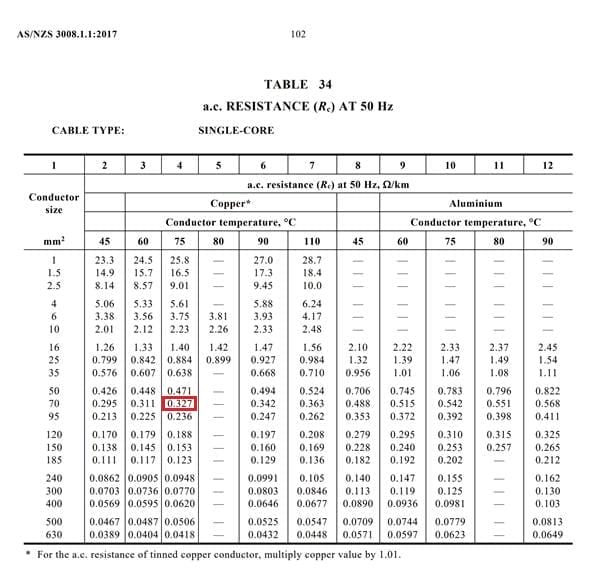
En utilisant le tableau 34 (voir l'annexe 1 ci-dessous), nous pouvons trouver la résistance en courant alternatif du câble correspondant à la taille du conducteur et à la température du conducteur la plus proche de la température de fonctionnement du câble calculée à l'étape 1. Puisque nous avons calculé une température de 73,8°, nous devrions arrondir la température et supposer que 75° est la température la plus précise à utiliser.
Selon le tableau 34, la résistance d'un câble avec un conducteur en cuivre de 70 mm2 et une température de fonctionnement de 75° est de 0,327 Ω/km, soit 0,000327 Ω/m.
Étape 3 : Déterminer la réactance du câble
La réactance des câbles à âme unique dépend du type de câble et de la séparation des câbles.
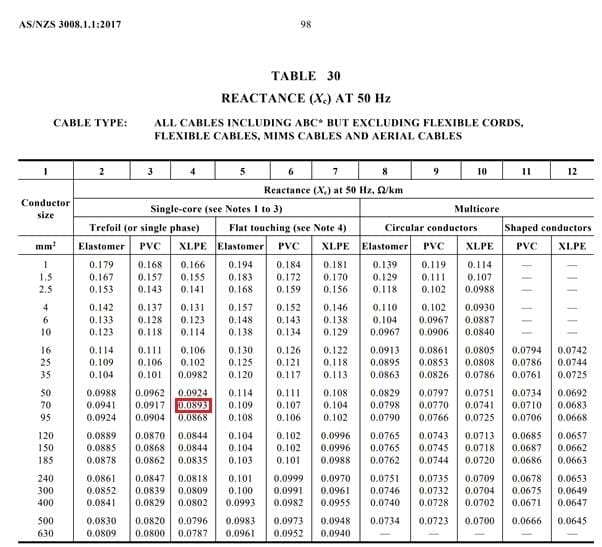
En utilisant le tableau 30 (voir l'annexe 2 ci-dessous), nous pouvons trouver la réactance à 50 Hz.
Nos câbles sont en forme de trèfle, donc d'après la colonne 3, la réactance du câble est de 0,0893 Ω/km , ou 0,0000893 Ω/m.
Étape 4 : Calculer la chute de tension en fonction du facteur de puissance et de la température de fonctionnement du câble
Nous utiliserons l'équation 3 pour calculer la chute de tension triphasée. Pour cela, nous avons besoin de l'angle de phase de la charge en fonction du facteur de puissance de la charge comme suit :
\N(\Ntheta = cos^{-1}(0,9)\N)
\(\theta = 25.84193276^{\circ} = 0.4510268 \; rads\)
\(sin\theta = 0.43588989\)
Nous disposons maintenant de tous les paramètres nécessaires pour calculer la chute de tension triphasée :
\(V_{d3\phi} = 250 \cdot 120[\sqrt{3}(0.000327 \cdot 0.9 + 0.0000893 \cdot 0.43588989)]\c)
\(V_{d3\phi} = 17.315 \; V\)
La chute de tension en pourcentage de la tension d'alimentation est de 17,315 / 400 V, soit 4,33%.
Annexes
Annexe 1 - Tableau 34 avec la valeur pertinente surlignée en rouge
Annexe 2 - Tableau 30 avec la valeur pertinente surlignée en rouge